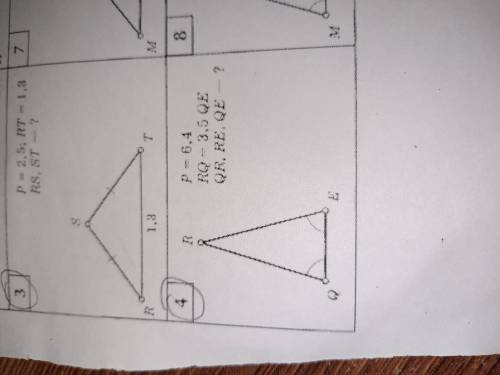
решить 4 пример Дано: треугольник

P=6,4

RQ=3,5 QE

Найти:

QR,RE,QE-?

4) Так как углы при основании равны, то треугольник равнобедренный и RQ=RE;

P=RQ+RE+QE

RQ=3,5QE; => RE=3,5QE

6,4=3,5QE+3,5QE+QE

8QE=6,4

QE=0,8; =>

RQ=RE=0,8*3,5=2,8.

ответ: QE=0,8; QR=RE=2,8.

Объяснение:

=> - Значок следовательно.

Для решения данной задачи, мы можем использовать теорему Пифагора и свойства треугольника.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

В данной задаче у нас нет информации о том, является ли треугольник прямоугольным, поэтому мы не можем применить теорему Пифагора напрямую.

Однако, у нас есть значение стороны PQ, которое равно 6,4. Мы можем использовать это значение для решения задачи.

Первым шагом, найдем значение стороны QR с использованием теоремы Пифагора.

Мы знаем, что сторона RQ равна 3,5 и сторона QE равна 6,4.

Поэтому, используя теорему Пифагора, мы можем записать:

QR^2 = RQ^2 + QE^2

QR^2 = 3,5^2 + 6,4^2

QR^2 = 12,25 + 40,96

QR^2 = 53,21

На этом этапе мы получили значение для QR в квадрате, чтобы найти само значение, нам нужно извлечь квадратный корень:

QR = √53,21

QR ≈ 7,29 (округление до сотых)

Теперь мы можем перейти ко второму шагу, чтобы найти значение для стороны RE.

Согласно свойствам треугольника, сумма длин двух сторон всегда больше длины третьей стороны. Поэтому, чтобы получить значение RE, мы должны вычесть длину стороны QR из суммы длин сторон RQ и QE:

RE = RQ + QE - QR

RE = 3,5 + 6,4 - 7,29

RE ≈ 9,71 - 7,29

RE ≈ 2,42 (округление до сотых)

И, наконец, чтобы найти значение стороны QE, нам просто нужно использовать значение, данное в условии:

QE = 6,4

Таким образом, мы получаем следующие значения:

QR ≈ 7,29
RE ≈ 2,42
QE = 6,4