решить 1. В прямоугольную трапецию с острым углом 30 градусов вписали окружность радиус которой равен 6 см. Найди периметр трапеции
2. Сумма двух углов четырехугольника, вписанного в окружность, равна 185 градусов а разность этих же углов равна 155 градусов. Найди все углы четырехугольника
3.Трапецию вписали в окружность. Меньшее основание отсекает окружности дугу 15 градусов а боковая сторона отсекает дугу 20 градусов. Найди градусную меру дуги, которую отсекает от окружности большее основание трапеции.

1) Периметр трапеции ABCD равен 72 см.

2) Углы четырехугольника, вписанного в окружность:

∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.

3)Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.

Объяснение:

1) Требуется найти периметр прямоугольной трапеции, в которую вписали окружность.

Дано: АВСД - прямоугольная трапеция.

Окр.О,R;

∠D=30°;

ОМ = 6 см.

Найти: .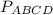

Для того, чтобы найти периметр, необходимо найти все стороны трапеции.

1. Рассмотрим АВРК.

Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ АВРК - прямоугольник.

AB = 2R = 6*2 = 12 (см)

Противоположные стороны прямоугольника равны.

ВР = АК = R = 6 см

2. Рассмотрим ΔНСD - прямоугольный (СН - высота).

∠D = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ CD = 2*CH = 12 * 2 = 24 (см)

3. CD = CE + ED = 24 см.

Отрезки касательных к окружности, проведенные из одной точки, равны.

⇒ PC = CE; KD = DE.

или РС + KD = 24 см.

4. Теперь найдем периметр трапеции ABCD.

Периметр - сумма длин всех сторон.

= AB + BC + CD + AD = AB +BP + PC + CD + AK + KD =

= 12 + 6 + 24 +24 + 6 = 72 (см)

Периметр трапеции ABCD равен 72 см.

2) Требуется найди все углы четырехугольника, вписанного в окружность.

Дано: ABCD - вписанный четырехугольник.

∠C + ∠D = 185°; ∠C - ∠D = 155°

Найти: ∠A; ∠B; ∠C; ∠D.

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна 180°.

Так нам дана сумма углов, равная 185°, то рассматривать противоположные углы мы не можем. Поэтому выбрали ∠С и ∠D.

1. По условию

∠C + ∠D = 185°

∠C - ∠D = 155°

Сложив эти два уравнения, получим:

2∠С = 340°   |:2

∠C = 170°

Подставив это значение в любое из уравнений, получим

∠D = 15°

2. Теперь найдем остальные углы четырехугольника, вписанного в окружность.

∠A + ∠C = 180°   ⇒   ∠A = 180° - 170° = 10°

∠B + ∠D = 180°   ⇒   ∠B = 180° - 15° = 165°

Углы четырехугольника, вписанного в окружность:

∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.

3) Требуется найди градусную меру дуги, которую отсекает от окружности большее основание трапеции.

Дано: Окр.О;

ABCD - трапеция, вписанная  в окружность.

∪АВ = 20°; ∪ВС = 15°

Найти: ∪АmD.

Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

⇒ ABCD - равнобедренная трапеция, то есть

AB = CD.

Равные хорды стягивают равные дуги.

⇒ ∪АВ = ∪CD = 20°

Градусная мера всей окружности равна 360 °.

⇒  ∪АmD = 360° - (∪АВ + ∪ВС +∪CD) = 360° - 55° = 305°

Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.