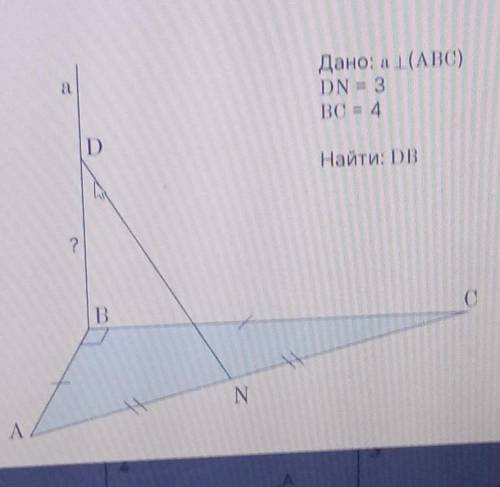
Реши задачу, исходя из данных рисунка. а Дано: а перпендикулярна (ABC) DN = 3 BC = 4 D Найти: DB

Ответы

vihshgfgvf 19.03.2022 16:31

DB= 1 ед.

Объяснение:

Рассмотрим рисунок. Треугольник Δ АВС - прямоугольный, так как ∠В=90° и равнобедренный, так как АВ=ВС. По условию АВ=ВС=4 ед.

Найдем гипотенузу АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AC^{2} =AB^{2} +BC^{2} ;\\AC= \sqrt{AB^{2} +BC^{2}} ;\\AC= \sqrt{4^{2} +4^{2} } =\sqrt{16+16} =\sqrt{16\cdot2} =4\sqrt{2}$

По рисунку понятно, что N- середина АС и тогда отрезок BN - медиана прямоугольного треугольника АВС.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.

Значит,

$BN= \dfrac{1}{2} AC;\\\\BN= \dfrac{1}{2} \cdot4\sqrt{2} =2\sqrt{2}$

Так как по условию а ⊥ (АВС), то она перпендикулярна любой прямой, лежащей в этой плоскости.

Тогда а⊥ BN и ΔDBN - прямоугольный.

Применим теорему Пифагора и найдем DB.

$DB^{2} =DN^{2} -BN^{2} ;\\DB= \sqrt{DN^{2} -BN^{2}} ;\\DB=\sqrt{3^{2} -(2\sqrt{2})^{2} } =\sqrt{9-8} =\sqrt{1} =1$

DB= 1 ед.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

АуTист 06.04.2020 12:23

bengamin1993 06.04.2020 12:21

Знайти радіус кола площа якого 28.26...

eon1986 06.04.2020 12:22

anastasikot 06.04.2020 12:22

MrHezbollah 06.04.2020 12:22

Ребята очень нужен ваш ответ!...

nastorekhova20 06.04.2020 12:22

misterkorolev0 06.04.2020 12:19

Вика00000011 06.04.2020 12:20

RokiFoki 06.04.2020 12:19

Геометрия. 8кл. Надо решение данной задачи ребята?...

donik223 06.04.2020 12:17