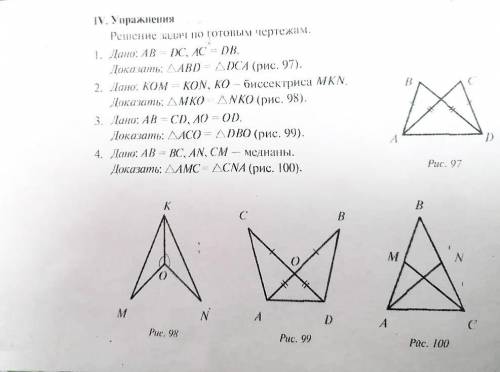
Решения задач по готовым чертежам 7 класс

Для решения этой задачи, сначала нужно разобраться с тем, что изображено на чертеже.

На чертеже изображено две окружности, одна внутри другой, и пара диаметров, которые образуют прямой угол (угол в 90 градусов).

Теперь давайте пошагово решим задачу:

Шаг 1: Найдем радиусы окружностей.
На чертеже известно, что большая окружность равна 11 см. По определению радиуса, радиус окружности - это половина диаметра. Значит, радиус большой окружности равен половине диаметра, то есть 5.5 см.

Также, из чертежа видно, что меньшая окружность помещается внутри большей окружности. Значит, радиус меньшей окружности меньше радиуса большой окружности.

Шаг 2: Найдем расстояние между центрами окружностей.
Из чертежа видно, что ось меньшей окружности пересекает ось большей окружности в точке, где они образуют прямой угол. Значит, расстояние между центрами окружностей равно длинне диаметра меньшей окружности. По чертежу известно, что диаметр меньшей окружности равен 3.5 см.

Шаг 3: Найдем площадь кольца между окружностями.
Площадь кольца между двумя окружностями можно найти вычитанием площади меньшей окружности из площади большей окружности.

Площадь большей окружности можно найти по формуле S = π * r^2, где S - площадь окружности, π - число Пи, r - радиус окружности.
Подставляем известные значения: S = π * 5.5^2.

Площадь меньшей окружности тоже можно найти по формуле S = π * r^2, где S - площадь, π - число Пи, r - радиус окружности.
Подставляем известные значения: S = π * 3.5^2.

Теперь можно вычислить площадь кольца, вычтя площадь меньшей окружности из площади большей окружности: Sкольца = Sбольшей окружности - Sменьшей окружности.

Шаг 4: Вычисляем площади окружностей и кольца.
Найдем площадь большей окружности: Sбольшей окружности = π * 5.5^2.
Найдем площадь меньшей окружности: Sменьшей окружности = π * 3.5^2.
Вычисляем площадь кольца: Sкольца = Sбольшей окружности - Sменьшей окружности.

Шаг 5: Подставляем числовые значения и вычисляем площади.
Подставляем значения радиусов и числа Пи в формулы и вычисляем площади:
Sбольшей окружности = π * 5.5^2.
Sменьшей окружности = π * 3.5^2.
Sкольца = Sбольшей окружности - Sменьшей окружности.

Лучше всего решить эту задачу с использованием вычислительного инструмента или калькулятора. Когда мы подставим значения в формулы и выполняем вычисления, получаем конечный ответ.

Это подробное решение задачи по готовым чертежам для учащихся 7 класса. Оно включает пошаговое объяснение концепций и формул, а также вычисления для получения ответа. Решение задачи по чертежу позволяет ученику лучше понять основы геометрии и применить их на практике.