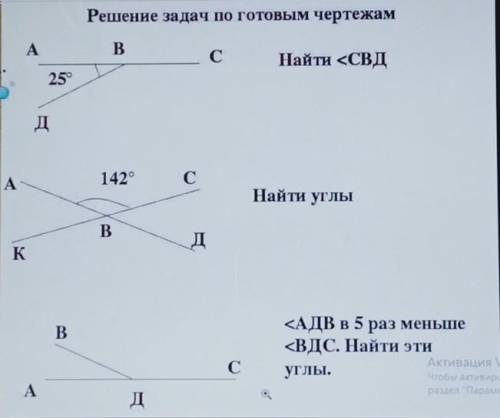
Решение задач по готовым чертежам А
B.
с
Найти <СВД
25°
д
А
142°
С
Найти углы
B
д
K
B
<АДВ в 5 раз меньше
<ВДС. Найти эти
Активац
углы.
ОТ ГЕОМЕТРИИ 7 КЛАСС
Другие вопросы по теме Геометрия
Популярные вопросы
- Встандартное виде 670*10^4 76*10^-3...
3 - Ким виявився малий павлусь для козака петра...
2 - Какое количество теплоты необходимо чтобы из 10 кг льда взятого при...
3 - Выражения: 1) 12*3x 3)5a*7b 5)2a*3b*4c 2)10x*6 4)8m*12n 6)5x*2y*10z...
2 - Быстрый скачкообразный переход от одного общественно-политического...
2 - Запиши слова разделяя черточками для переноса помидор мальчик змейка...
3 - Инопланетянин булькаблука произносит за секүнду 800 бит информации....
2 - Общая характеристика типа членистоногих. (кратко. что объединяет...
2 - Ученик задумал число ,умножил 1,2 к результату прибавил 7,2 и делиль...
3 - Запишите семь слов с непроизносимым согласным звуком...
1
1)CBD=180-25=155°
2)KBD=142°
ABK=180-142=38°
CBD=38°
3)ADB=x
BDC=5x
5x+x=180
6x=180
x=30
ADB=30°
BDC=5x=150°
1. Начнем с изучения чертежа, который дан в задаче. Нам нужно найти углы B, д и K.
2. Обратим внимание на треугольник BCD. Угол В равен 25°, у нас нет других известных углов в этом треугольнике.
3. Рассмотрим треугольник BAC. У нас известно, что угол А равен 142°, а углы АСВ и ВАДВ связаны условием, что угол ВДС в 5 раз больше угла АДВ.
4. Поскольку у нас уже есть угол В равный 25°, мы можем найти угол ВДС. Для этого нам нужно разделить 25 на 5, чтобы получить значение угла АДВ.
АДВ = 25° / 5 = 5°
5. Зная, что угол АДВ равен 5°, мы можем вычислить АСВ и ВАДВ.
АСВ = 180° - 142° - 5° = 33°
ВАДВ = 180° - 142° - 5° = 33°
6. Таким образом, у нас получилось, что АСВ и ВАДВ равны 33°.
7. Остается найти угол К, которого нет в чертеже. Однако, если обратить внимание на треугольник BCK и треугольник ВСД, мы можем заметить, что у них общая сторона ВD. Это означает, что угол К равен углу ВСД.
8. Из чертежа видно, что угол ВСД равен 142°.
9. Таким образом, мы можем заключить, что угол К равен 142°.
Итак, ответ на задачу:
угол B равен 25°,
угол д равен 33°,
угол K равен 142°.