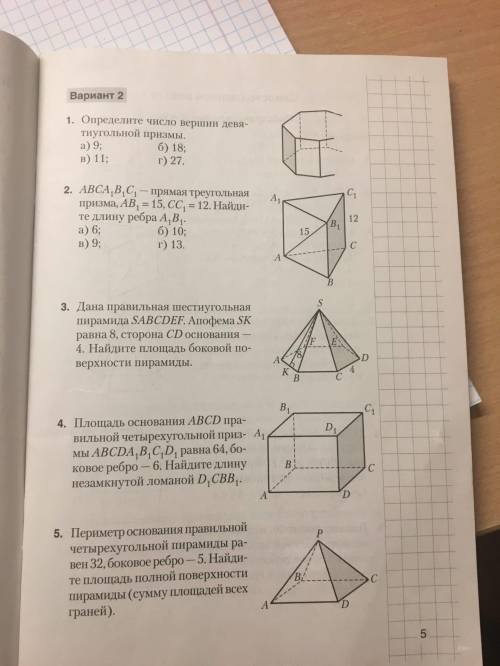
Ребят кто может пропустила тему ни черта не понимаю 2. АВСА В С - прямая треугольная призма, АВ, = 15, СМ, = 12. Найдите длину ребра А В
a) 6; б) 10;
b) 9; г) 13.
15
в, 12
3. Дана правильная шестиугольная пирамида SABCDEF. Апофема SK равна 8, сторона CD основания -
4. Найдите площадь боковой поверхности пирамиды.
4. Площадь основания ABCD пра-
вильной четырехугольной приз- А мы ABCDA, B, C,D, равна 64, боковое ребро - 6. Найдите длину незамкнутой ломаной D CBB
5. Периметроснования правильной четырехугольной пирамиды равен 32, боковое ребро - 5. Найдите площадь полной поверхности пирамиды (сумму площадей всех граней).

Добрый день! Давайте рассмотрим каждый вопрос по очереди.

1. Для начала найдем длину ребра АВ в треугольной призме АВСАВС. У нас известны значения АВ = 15 и СМ = 12. Ребра АВ и СМ соединены перпендикулярно, так как призма треугольная. Для нахождения длины ребра АВ можно использовать теорему Пифагора, так как у нас есть прямоугольный треугольник с гипотенузой АВ.

Используя теорему Пифагора, мы можем найти длину ребра АВ:
(АВ)^2 = (СМ)^2 + (АС)^2
(АВ)^2 = 12^2 + 15^2
(АВ)^2 = 144 + 225
(АВ)^2 = 369

Чтобы найти значение ребра АВ, возьмем квадратный корень из обоих частей уравнения:
АВ = √369

Мы не можем найти точное значение квадратного корня из 369, но мы можем приближенно рассчитать его.

Проверим каждый вариант ответа:
а) 6: Не верно, так как 6^2 = 36, что меньше 369.
б) 10: Не верно, так как 10^2 = 100, что меньше 369.
в) 9: Не верно, так как 9^2 = 81, что меньше 369.
г) 13: Верно, так как 13^2 = 169, что больше 369.

Таким образом, длина ребра АВ равна 13.

2. Дана правильная шестиугольная пирамида SABCDEF. Апофема SK равна 8, а сторона CD основания равна 4. Для нахождения площади боковой поверхности пирамиды нам нужно использовать формулу:

Площадь боковой поверхности = Периметр основания * Апофема / 2.

Основание пирамиды - шестиугольник, значит у него 6 сторон. Чтобы найти периметр основания, нужно умножить длину одной стороны на количество сторон. В данном случае, у нас сторона CD равна 4, а количество сторон 6, поэтому периметр основания равен 4 * 6 = 24.

Теперь мы можем подставить значения в формулу:
Площадь боковой поверхности = 24 * 8 / 2
Площадь боковой поверхности = 192 / 2
Площадь боковой поверхности = 96.

Площадь боковой поверхности пирамиды равна 96.

3. Дана правильная четырехугольная пирамида ABCDA, B, C, D. Площадь основания ABCD равна 64, а боковое ребро равно 6. Найдем длину незамкнутой ломаной DCBB.

Поскольку пирамида правильная, то у нее все стороны основания равны. Значит, можно найти длину каждой стороны основания ABCD, разделив площадь основания наыыы на количество сторон. В данном случае, у нас четырехугольник, а значит четыре стороны. Площадь ABCD = 64, поэтому длина стороны основания равна √(64/4) = √16 = 4.

Теперь рассмотрим ломаную DCBB. Для начала нарисуем пирамиду ABCDA с боковыми ребрами:

A
/ \
/ \
/ \
D-------B
|-------|
\ /
\ /
\ /
C

Мы хотим найти длину незамкнутой ломаной DCBB. Нам уже известно, что ребро Б находится на грани-основании AD, значит длина отрезка DCB равна длине ребра (6).

Теперь осталось найти длину отрезка BD. Для этого воспользуемся теоремой Пифагора для прямоугольного треугольника ABD, где АВ - гипотенуза:

(АВ)^2 = (АС)^2 + (СВ)^2
(АВ)^2 = (4)^2 + (4)^2
(АВ)^2 = 16 + 16
(АВ)^2 = 32

Теперь найдем длину ребра ВD, взяв квадратный корень из обеих частей уравнения:
BD = √32

Таким образом, длина незамкнутой ломаной DCBB равна 6 + √32.

4. Дана правильная четырехугольная пирамида ABCDA, B, C, D. Периметр основания равен 32, а боковое ребро равно 5. Найдите площадь полной поверхности пирамиды (сумму площадей всех граней).

Для решения этого вопроса нам нужно найти площадь каждой грани пирамиды и сложить их.

Основанием пирамиды является четырехугольник ABCD. Периметр основания равен 32, а значит сторона основания равна 32/4 = 8 (так как у нас четырехугольник).

Теперь найдем площадь боковых граней. Площадь каждой боковой грани треугольной пирамиды можно найти, используя формулу:

Площадь боковой грани = (Периметр основания * Апофема) / 2.

У нас уже известно, что боковое ребро равно 5. Чтобы найти апофему пирамиды, нужно воспользоваться теоремой Пифагора для прямоугольного треугольника ACB, где СМ - гипотенуза:

(АС)^2 = (АВ)^2 + (СМ)^2
(АС)^2 = (8)^2 + (5)^2
(АС)^2 = 64 + 25
(АС)^2 = 89

Теперь найдем длину апофемы СВ, взяв квадратный корень из обеих частей уравнения:
СВ = √89.

Теперь можем посчитать площадь каждой боковой грани:
Площадь боковой грани = (8 * √89) / 2 = 4 * √89.

Таким образом, площадь всех боковых граней равна 4 * √89 * 4 = 16 * √89.

Теперь нам осталось найти площадь основания. Мы уже знаем, что сторона основания равна 8. Площадь четырехугольника ABCD можно найти, используя формулу для площади прямоугольника:

Площадь основания = (сторона АВ) * (сторона АС) = 8 * 8 = 64.

Теперь мы можем найти площадь полной поверхности, суммируя все найденные площади:
Площадь полной поверхности = Площадь основания + Площадь боковых граней = 64 + 16 * √89.

Таким образом, площадь полной поверхности пирамиды равна 64 + 16 * √89.

Я надеюсь, что эти пошаговые решения помогут вам лучше понять материал! Если у вас возникнут еще вопросы, не стесняйтесь спрашивать. Я всегда готов помочь!