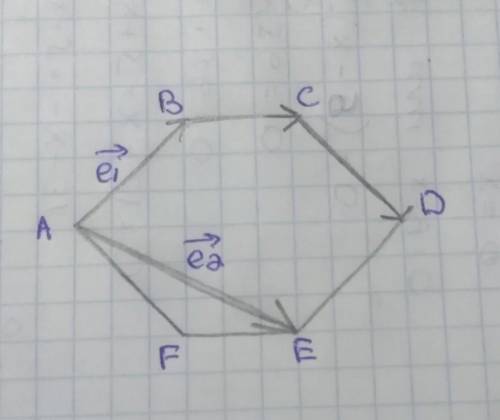
Разложить в базисе (е1, е2) вектора :
BC, CD
Другие вопросы по теме Геометрия
Популярные вопросы
- Мотоциклист едет со скоростью 45 км в час,какое расстояние он...
1 - Какие из этих чисел составные 431,437,467,587,667,677,703,713,739,899,907....
1 - Почему при определенной концентрации углекислого газа в крови...
1 - Найти пейзажи в сказке паустовского теплый хлеб ....
2 - Хелп! кто сколько сможет! 53,5: 5 1,75: 7 0,48: 6 13,2: 24 0,7:...
2 - Вставьте слово: if you borrow the money, you should pay 1)again...
3 - Крылатые выражения и фразы в комедии ревезор...
2 - 1)какие крестьяне считались временно обязанными: а. крестьяне,...
3 - Укажите собирательные существительные: 1. молодёжь 2. детвора...
3 - Составить программу печатающую значение true если указанное...
3
Давайте начнем с вектора BC.
1. Найдем координаты начала и конца вектора BC:
- Координаты начала вектора BC: A = (1, 2)
- Координаты конца вектора BC: B = (3, 4)
2. Найдем базисные векторы:
- e1 - это вектор, который соединяет точки A и C
- e2 - это вектор, который соединяет точки A и D
3. Найдем координаты базисных векторов:
- Координаты базисного вектора e1: AC = B - A = (3, 4) - (1, 2) = (2, 2)
- Координаты базисного вектора e2: AD = D - A = (5, 6) - (1, 2) = (4, 4)
4. Запишем систему уравнений для разложения вектора BC в базисе (е1, е2):
BC = αe1 + βe2
5. Решим систему уравнений:
Заменим координаты вектора BC и базисных векторов:
(3, 4) = α(2, 2) + β(4, 4)
Распишем умножение вектора на скаляр:
(3, 4) = (2α, 2α) + (4β, 4β)
Распишем сложение векторов:
(3, 4) = (2α + 4β, 2α + 4β)
Получаем систему уравнений:
2α + 4β = 3
2α + 4β = 4
Поскольку первое и второе уравнения совпадают, у нас есть только одно уравнение с двумя неизвестными.
Мы не можем однозначно определить значения α и β на основе этой системы.
6. Заключение:
Из системы уравнений мы не можем найти значения α и β для разложения вектора BC в базисе (е1, е2). Вероятно, была допущена ошибка в исходных данных или пропущен какой-то дополнительный шаг для решения этой задачи.
Ответ: Невозможно разложить вектора BC в базисе (е1, е2) без дополнительных данных или исправления исходной задачи.