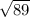Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны по 10 см, а сторона основания AE= 12 см. К этой плоскости проведены перпендикуляр CB, который равен 5 см, и наклонные CA и CE. Вычисли расстояние от точки C до стороны треугольника AE
Другие вопросы по теме Геометрия
Популярные вопросы
- ⚫ Найди в тексте 4 орфографические ошибки и 1 пунктуационную. ⚫...
3 - Цель: с подручных средств пронаблюдать и объяснить явление интерференции...
1 - с задвниями 1477,1478,1479.1480...
1 - Сочинение почему семья нужна человеку (на основе рассказа алексина...
2 - Я ВАС Сравнить числа: а) 21,451 и 21,5629 б) 0,8647 и 0,999 в)...
1 - Даны вектора a(3; 4; 5) и b(4;2; 5) . Будут ли коллинеарными векторы...
1 - Через які канали можна подавати призентацію...
1 - коли виникають звукові хвилі більшої амплітуди під час старту космічної...
3 - Поздние мифы рассказывают о …….Древние мифы продолжают …..В хрестоматии...
2 - Вычислите сумму чисел в MS Excel. 1. 258; 87; 1362; 75,6 2. 258;...
2
Объяснение:
рассматриваем ΔABC и ΔEBC, они прямоугольные, тк CB перпендикуляр. По теореме Пифагора находим АС=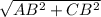 и ЕС=
и ЕС=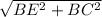 подставляем АС=
подставляем АС=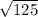 =5
=5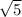 , EC=
, EC=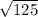 =5
=5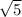 . Значит ΔACE равнобедренный, значит искомая высота СF является и медианой. AF=AE/2=6. Рассмотрим прямоугольный ΔСFA, найдем CF по теореме Пифагора
. Значит ΔACE равнобедренный, значит искомая высота СF является и медианой. AF=AE/2=6. Рассмотрим прямоугольный ΔСFA, найдем CF по теореме Пифагора
=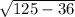 =
=