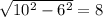Расстояние от т. s до каждой из вершин правильного треугольника abc равно 10 см. найдите расстояние от т. s до плоскости треугольника, если его медиана равна 9см. тут как-то вроде связано с радиусом описаной окружности, выручайте, кто понимает.

Значит расстояние до плосктсти это высота пирамиды ABCS. Так как треугольник ппавильный ( это который равносторонний?), то конец высоты на плоскости треугольника центр описанной окружности и является цетром пересечения медиан биссектрис, высот...

Берем медиану она делится точкой пересечения в отношении 2 к 1, то есть одна часть будет 6, а другая 3. Там далее вырисовывается прямоугольный треугольник образованный ребром, высотой , и частю медианы длинной 6, то высота по теорме Пифагора