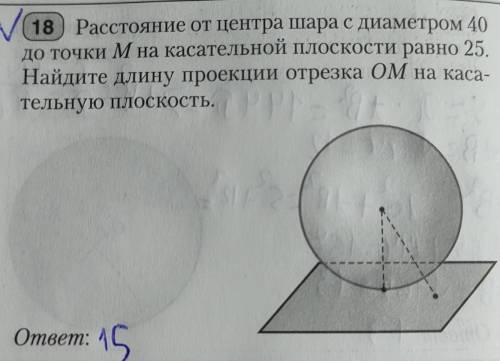
Расстояние от центра шара с диаметром 40 до точки M на касательной плоскости равно 25.Найдите длину проекции отрезка OM на касательную плоскость

Для начала, давайте разберемся в том, какими свойствами обладает касательная плоскость к шару.

1. Касательная плоскость к шару проходит через точку касания с поверхностью шара. В данном случае, точка M является точкой касания.

2. Касательная плоскость к шару перпендикулярна радиусу, проведенному из центра шара и проходящему через точку касания. В нашем случае, радиусом будет отрезок OM.

Теперь, чтобы найти длину проекции отрезка OM на касательную плоскость, мы можем воспользоваться теоремой Пифагора. Ведь у нас есть прямоугольный треугольник, в котором одна сторона равна расстоянию от центра шара до точки M, другая сторона равна длине радиуса шара, а третья сторона - искомая проекция отрезка OM.

Давайте обозначим расстояние от центра шара до точки M, как a (в нашем случае a = 25), а радиус шара - r (в нашем случае r = 20, так как диаметр шара равен 40).

Используя теорему Пифагора, мы можем записать:

a^2 + b^2 = c^2,

где a - расстояние от центра шара до точки M, b - длина проекции отрезка OM на касательную плоскость, c - длина радиуса шара.

Подставляя известные значения, получаем:

25^2 + b^2 = 20^2.

Выполняя простые математические операции, получаем:

625 + b^2 = 400.

Вычитая 400 из обеих сторон уравнения, получаем:

b^2 = 225.

Извлекая квадратный корень, получаем:

b = √225.

Так как нас интересует только положительное значение b, то окончательный ответ:

b = 15.

Таким образом, длина проекции отрезка OM на касательную плоскость равна 15.