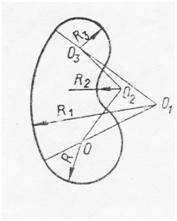
Расстояние между центрами О и О1 равно:

Для решения этой задачи нам потребуется использовать свойства окружностей и треугольников.

Итак, у нас дана картинка с двумя окружностями, центры которых обозначены символами O и O1. Нам нужно найти расстояние между этими центрами.

1. Прежде всего, обратимся к свойству окружностей. Это свойство гласит, что радиус окружности перпендикулярен к хорде (отрезку, соединяющему две точки окружности). В нашем случае точки O и O1 являются центрами окружностей, поэтому отрезок OО1 является прямым радиусом окружностей.

2. Возьмем две точки пересечения окружностей A и B. Образуется прямоугольный треугольник OАВ, где О - вершина прямого угла, ОА и ОВ - радиусы окружностей, AВ - хорда, искомая величина.

3. Пользуясь свойством окружности о перпендикулярности радиуса к хорде, можно сделать вывод, что угол ОАВ - прямой. Тогда, с помощью теоремы Пифагора, можно выразить длину хорды AВ:

(ОА)^2 + (ОВ)^2 = (АВ)^2.

4. Для вычисления хорды AВ нам понадобятся еще значения ОА и ОВ, то есть радиусы окружностей. В задаче они явно не указаны, поэтому нам потребуется дополнительная информация для решения задачи.

Если радиусы окружностей известны, мы можем заменить их значениями и рассчитать длину хорды AВ. Если других данных нет, то ответ на вопрос о расстоянии между центрами О и О1 будет неопределенным.

Важно помнить, что свойства окружностей могут быть использованы для решения различных задач. В данном случае нам потребуется знать значения радиусов или другую информацию для получения точного ответа.