Радиусы оснований усечённого конуса равны r и r, а образующая наклонена к плоскости основания под углом . найти площадь его боковой поверхности.
Ответы
Площадь боковой поверхности конуса равна 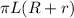 , где
, где 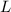 - длина образующей. В этой задаче
- длина образующей. В этой задаче 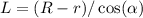 . Поэтому площадь боковой поверхности равна
. Поэтому площадь боковой поверхности равна 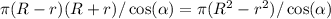 ,
,
ПОКАЗАТЬ ОТВЕТЫ
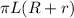 , где
, где 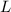 - длина образующей. В этой задаче
- длина образующей. В этой задаче 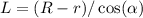 . Поэтому площадь боковой поверхности равна
. Поэтому площадь боковой поверхности равна 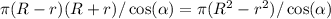 ,
,
Другие вопросы по теме Геометрия
Популярные вопросы
- Какую мощность развивает тяжелоатлет если за 2 секунды поднимает...
1 - Риси, притаманні і класицизму, і бароко:а) поєднання релігійних...
2 - На візок масою m, що рухається горизонтальними рейками зі швидкістю...
1 - На одній автостоянці було в 3 рази (-ів) менше машин, ніж на іншій....
1 - Определи: является ли корнем уравнения 13x+12=x число если не знаете...
1 - Сообщение «Художественное произведение – это диалог между художником...
2 - Початковий і середній рівні: 1) Визначити суму індексів в аміноетановій...
3 - Составить 4-5 предложений с данными словосочетаниями:freedom of...
1 - 15км220м+30км47м+18км60м+10км690м 3т805кг+14т70кг+20т16кг-35т804кг-6ц...
1 - Захотеть какой вид? Скажите...
3