Радиус основания конуса 5, а высота 12. плоскость сечения проходит через вершину конуса и хорду основания, длина которой 6. найдите расстояние от центра основания до плоскости сечения

Расстоянием от центра до плоскости будет ОL. ОL перпендикулярна плоскости ABS. Так как OL перпендикулярна SM по постороению.Также OL перпендикулярна АВ. AB перпендикулярна всей плоскости SOM по теореме о 3-х перпендикулярах. Значит и  Если прямая перпендикулярна двум непараллельным прямым в плоскости, то она перпендикулярна всей плоскости.

Рассмотрим треугольник SOM. Он - прямоугольный. Теперь найдем неизвестный катет ОМ. Его можно узнать из прямоугольного треугольника в основании конуса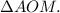 Так как АМ=МВ=3, так как SM - является высотой, биссектрисой и медианой в равнобедренном треугольнике ASB (AS=BS).  

У треугольника АОМ гипотенуза ОА=5 см, АМ=3см. Надо узнать только ОМ. По теореме Пифагора

Теперь снова обратим внимание на треугольник SOM. Два катета у него уже известны. SO=12 см как высота конуса. Теперь найдем гипотенузу SM по той же теореме Пифагора.

Найдем синус угла М в треугольнике SOM.

Теперь из прямоугольного треугольника MOL найдем катет OL, зная гипотенузу ОМ.

ответ: расстояние от точки О до плоскости сечения равно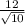

Есть конус. т.О - центр основания, Д - вершина, АВ - хорда.

Рассмотрим равнобедренный треугольник АВО: АО=ВО=r=5, АВ=6. Из т.О опустим перпендикуляр ОС к стороне АВ:

ОС^2=AO^2-AC^2=5^2-(6/2)^2=25-9=16, ОС=4.

Рассмотрим прямоугольный треугольник СДО: 

СД^2=OC^2+ОД^2=4^2+12^2=16+144=160, СД=4*корень из 10 

Из т.О проведем перпендикуляр ОЕ к стороне СД. Треугольники СДО и ЕДО подобны (угол Д общий, угол СОД=ОЕД=90). Тогда:

СД:ОД=ОС:ОЕ;

ОЕ=ОД*ОС/СД=12*4/(4*корень из 10)=12/корень из 10