Радиус окружности, вписанной в треугольник abc, равен 22 см. расстояние от центра о этой окружности до вершин a и b равны oa=77см, ob=33см. найти расстояние oc.

                Решение : /////////////////////////////////////

1)Найдём BP и AK по теореме Пифагора:

BP=√BO²-OP²=√33²-22²=11√5

AK=√AO²-OK²=√77²-22²=33√5

Отсюда можно найти AB=33√5+11√5=44√5

2)Заметим, что BH=BP(как отрезки касательных,проведённых из одной точки)

Вспомним, что центр вписанной окр.-точка пересечения биссектрис треугольника, поэтому найдём синус угла ABC, используя этот факт:

sin2α=2sinαcosα=2*=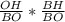

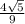
Пусть CP=CK=x,

Тогда SΔ=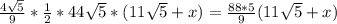    

С другой стороны, SΔ=S(ABO)+S(AOC)+S(BOC)

SΔ=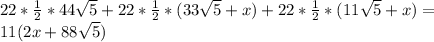

Приравнивая два вышенаписанных выражения для площади, найдём, что x=16.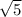

3)Тогда CO можно найти по теореме Пифагора:

CO=√OK²+CK²= √196*9=42