Радиус к вписанной окружности треугольника на рисунке равен: а) 2см
в) 3см
б) 2,5см
г) 8,5см
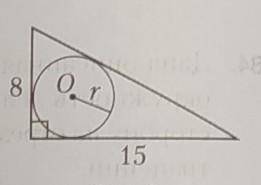
Другие вопросы по теме Геометрия
Популярные вопросы
- с английским 5. Заполните пропуски в тексте предложенными словами....
1 - 7. Почему тлей называют «дойнымикоровами»?...
2 - Заполните таблицу, перечислите не менее 2-х последствий (по каждой...
1 - Из 420 г 20%-го раствора сахарозы выпарили 80 г воды. Чему равна...
2 - Из за облаков пробиваются робкие лучи, но с каждым днём они становятся...
3 - 24 м 2. На рисунке дан планучастка. В каждом углуучастка разбиты...
3 - . Решите уравнение: 2|5x - 4|+ 8,6 = 10...
2 - установи соответствие между историческими событиями и их описанием...
2 - 5. По мнению ученых использование генно-модифицирова...ых культур...
3 - Известно, что дуб черешчатый- крупное дерево, части которого используются...
1
Во-первых, что такое вписанная окружность? Вписанная окружность - это окружность, которая касается всех сторон треугольника внутренним образом. В данном случае, у нас есть треугольник со сторонами a, b и c, и одна окружность, которая касается всех сторон.
Чтобы найти радиус вписанной окружности, нам понадобятся некоторые свойства треугольника. Одно из таких свойств - это формула радиуса вписанной окружности, которая связана с площадью треугольника и его полупериметром.
Формула выглядит следующим образом:
r = S / p,
где r - радиус вписанной окружности,
S - площадь треугольника,
p - полупериметр треугольника.
Чтобы решить задачу, нам нужно знать длины сторон треугольника. Посмотрим на рисунок.
Стартовая точка треугольника указана как A. У нас есть стороны, которые отмечены как a, b и c.
Вначале, нам нужно найти полупериметр треугольника. Полупериметр (p) можно найти, просуммировав все стороны треугольника и разделив полученную сумму на 2:
p = (a + b + c) / 2.
Далее, нам нужно найти площадь треугольника. Мы можем использовать формулу Герона для этого, так как у нас есть длины всех сторон:
S = √(p * (p-a) * (p-b) * (p-c)).
Теперь, когда у нас есть площадь треугольника и полупериметр, мы можем использовать формулу для радиуса вписанной окружности:
r = S / p.
Теперь давай применим все это к нашему треугольнику и найдем радиус вписанной окружности.
Мы видим, что у нас есть стороны a = 9 см, b = 12 см и c = 15 см. Давайте найдем полупериметр:
p = (a + b + c) / 2 = (9 + 12 + 15) / 2 = 36 / 2 = 18 см.
Теперь найдем площадь треугольника, используя формулу Герона:
S = √(p * (p-a) * (p-b) * (p-c)) = √(18 * (18-9) * (18-12) * (18-15)) = √(18 * 9 * 6 * 3) = √2916 = 54 см².
Теперь, найдем радиус вписанной окружности, используя формулу:
r = S / p = 54 / 18 = 3 см.
Таким образом, радиус вписанной окружности треугольника на рисунке равен 3 см.
Я надеюсь, что это ответ ясен и понятен для тебя! Если у тебя возникнут еще вопросы, не стесняйся задавать!