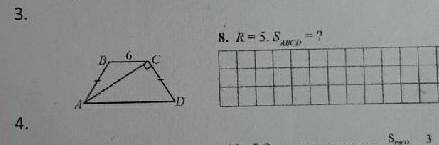
R описанной окружности = 5
BC = 6
Sabcd - ?​

Диагональ равнобокой трапеции ABCD перпендикулярна боковой стороне. Радиус окружности описанной около трапеции равен R=5 , ВС=6 . Найти площадь трапеции .

Объяснение:

Все вершины трапеции лежат на окружности , в том числе  вершины

Δ АCD - прямоугольного,  значит центр описанной окружности лежит на середине гипотенузы AD . Поэтому AD=2*R=2*5=10 (ед. изм.).

Пусть ВН⊥AD ,CK⊥AD , тогда НВСК-прямоугольник  и  ВС=НК=6 (ед.изм.).

Тогда КD=(AD-HK):2=(10-6):2=2( ед.изм.), Тогда АК=10-2=8 (ед.изм.)

Δ АCD -прямоугольный , т.к. высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу, то СК=√(2*8)=4 (ед.изм.)

S(ABCD)=1/2*CK*(AD+BC)

S(ABCD)=1/2*4*(6+10)=32(ед.изм.²)