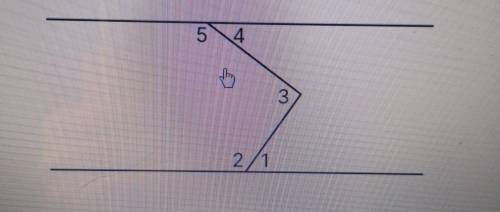
Прямые на рисунке параллельны. Найди градусную меру 25, если Z1 = 42°, а 23 = 75°. 54 му 3 2/1 2
Другие вопросы по теме Геометрия
Популярные вопросы
- 2. относительная влажность воздуха при нормальной температуре равна 60%.выпадет...
3 - Из точки к плоскости проведены две наклонные образующие со своими проекциями...
1 - Какую массу соли и воды необходимо взять для приготовления 1.3 гр 0.6%...
2 - Охарактеризуйте основные факторы внешней среды, влияющие на микроорганизмы....
3 - Отметьте на координатном луче ( числовом луче ) точки : d(1|9),e(5|9),m(8|9)...
3 - Как найти ускорение по 2 закону ньютона...
3 - Чому членистоногі мають обмежені розміри порівняно з хребетними тваринами?...
3 - Создайте эссе на одну из тем: - «xviii век – золотой век ». - заслуга...
3 - Какие соединения образуются при внутримолекулярной и межмолекулярной дегидратации...
2 - Почему людям важно относится друг к другу с любовью...
2
Свойство 1: Когда прямые параллельны, все соответствующие углы равны.
В нашей задаче у нас есть два вертикальных угла - Z1 и Z3 (они находятся напротив друг друга на пересечении параллельных прямых).
Угол Z1 = 42° (дано в условии задачи).
Угол Z3 = Z1 (по свойству 1) = 42°.
Свойство 2: Сумма углов, лежащих на одной прямой, равна 180°.
На рисунке у нас есть прямая AB, на которой лежат углы Z1 (известный нам угол), Z2 (у него мы ищем градусную меру) и Z3 (который мы уже нашли).
Угол Z1 + угол Z2 + угол Z3 = 180° (по свойству 2).
Подставляем известные значения:
42° + угол Z2 + 42° = 180°.
Теперь решим уравнение относительно неизвестного угла Z2:
угол Z2 + 42° = 180° - 42°,
угол Z2 + 42° = 138°.
Чтобы найти градусную меру угла Z2, вычтем 42° из обеих сторон уравнения:
угол Z2 = 138° - 42° = 96°.
Таким образом, градусная мера угла 25 равна 96°.
Окончательный ответ: угол 25 равен 96°.