Прямые m и n заданы уравнениями.Найдите значение s при котором прямые m и n перпендикулярны
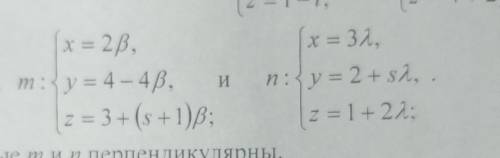
Ответы
Для того чтобы найти значение s, при котором прямые m и n перпендикулярны, необходимо использовать свойство перпендикулярных прямых: углы, образованные пересекающимися прямыми, равны между собой и сумма их углов равна 90 градусов.
Уравнения прямых m и n даны в виде:
m: y = -2x + 4
n: y = \(\frac{1}{2}\)x + s
Для начала, найдём угловые коэффициенты (наклоны) данных прямых. Угловой коэффициент прямой определяется коэффициентом при переменной x в уравнении прямой.
Для прямой m угловой коэффициент равен -2.
Для прямой n угловой коэффициент равен 1/2.
Перпендикулярные прямые имеют угловые коэффициенты, являющиеся обратно пропорциональными (-1/м), т.е. произведение угловых коэффициентов равно -1.
В данном случае, угловой коэффициент прямой m равен -2, следовательно, для прямой n угловой коэффициент должен быть равен -1/(-2) = 1/2.
Подставим этот угловой коэффициент в уравнение прямой n:
1/2 = \(\frac{1}{2}\)x + s
Теперь найдём значение s, при котором прямые m и n перпендикулярны. Для этого приравняем угловые коэффициенты прямых:
-2 = \(\frac{1}{2}\)
Уравнение не имеет решений, так как -2 не равно 1/2.
Таким образом, для данных уравнений прямых m и n, не существует значения s, при котором они будут перпендикулярны.
ПОКАЗАТЬ ОТВЕТЫ
Популярные вопросы
- Каков вклад исламской культуры в мировую цивилизацию?...
1 - Policeman: where were (be)you when you (see)the accident, sir? witness: i...
3 - Как записать решение : папа купил конфеты по 1 р. за шт. и столько же пироженых...
1 - 3.10.2016. сочинение на тему легко ли быть молодым 11 класс. самопридуманное,...
1 - Разделе звуки на гласные и согласные запишите их в два столбика aa,cc,dd,ee,gh,hh,ii,uu,vv,yy,oo,pp,qq,ss....
2 - Тишина нарушаемая только разноголосом щебетом укрывшихся в листве пташек действовало...
2 - Верёвку длиной 74 м разрезали на две части. длина первой части на 16 м длиннее...
3 - Назовите известные вам бактериальные заболевания. как эти заболевания? какие...
3 - Соедини рифмующие слова. like kite kim jake white bike cake swim...
1 - Подберите и запишите к даным словам проверочные слов а глаголы в времени в-зут...
1