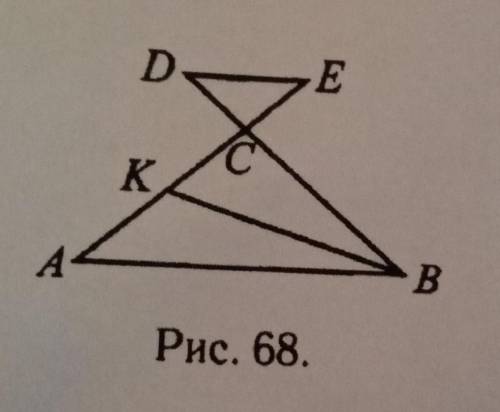
прямые DE и AB параллельно угол D= 50 градусов. Найдите угол ABC если BK биссектриса треугольника ABC​

Хорошо, давай разберем этот вопрос по шагам.

1. Первое, что нужно заметить, это то, что прямые DE и AB параллельны. Это означает, что угол DAB и угол EBC являются соответственными углами и равны между собой.

2. Также мы знаем, что угол D = 50 градусов. Поскольку угол DAB и угол EBC равны, то угол EBC тоже равен 50 градусов.

3. Посмотрим на треугольник ABC. У нас имеется биссектриса BK, которая разделяет угол ABC таким образом, что он делится на две равные части. Пусть угол ABK равен углу CBK и обозначим их обоих как х.

4. Теперь можем применить свойства биссектрисы. Согласно этому свойству, отношение длин сторон на основе AB и BC равно отношению синусов соответствующих углов, то есть AB / BC = sin(ABK) / sin(CBK). Но мы знаем, что AB / BC = sin(50) / sin(50), потому что углы ABK и CBK равны 50 градусам.

5. Теперь посчитаем эту дробь: sin(50) / sin(50) = 1. Таким образом, AB / BC = 1.

6. Это означает, что сторона AB равна стороне BC, поскольку отношение их длин равно 1.

7. Равные стороны треугольника ABC означают, что углы A и C равны между собой. Так как сумма углов треугольника равна 180 градусам, то оба этих угла A и C равны по 180 минус угол B. То есть угол A = угол C = 180 - угол ABC.

8. Зная, что угол A и угол C равны между собой, их сумма равна 180 градусам. Таким образом, 180 - угол ABC + угол ABC = 180 градусам.

9. Упрощая это уравнение, получаем 180 = 180, что всегда верно.

10. Значит, любое значение угла ABC удовлетворяет условию задачи. Мы не можем точно определить значение угла ABC, исходя только из предоставленной информации.