Прямые AB и CD параллельны.Докажите,что если отрезок BC пересекает прямую AD,то точка пересечения принадлежит отрезку AD.
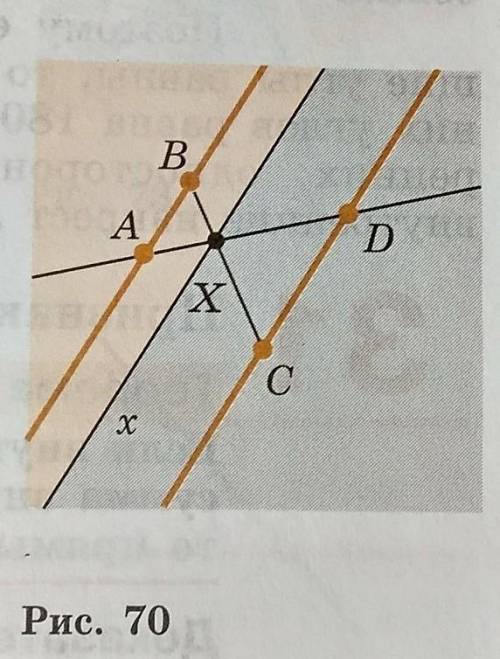
Другие вопросы по теме Геометрия
Популярные вопросы
- Задания суммативного оценивания за 4 четверть по предмету «Физика» 2...
3 - Ты знаешь что уже много лет ученые проверяют возможности людей и растения...
2 - Критичні точки функції y=x2-3x/x-4...
1 - 1. Какой частью речи являются слова я, ты, он, вы, они?А) Имя существительноеБ)...
2 - НУЖНО ОТВЕТЫ НА ЭТИ ВО Какие изменения произошли в управленческом аппарате...
3 - 1.В каких лакокрасочных материалах используется в качестве растворителя...
2 - На координатному промені з одиничним відрізком 2 см познач числа 3, 5...
3 - Соч по физике 9 класс 4 четверть...
1 - Установіть відповаідність між озерами та походженням їхніх улоговин:...
2 - Задача 1. Информационный объем сообщения 1,5 Мбайта, содержит 3145728...
1
Давайте рассмотрим данную ситуацию. У нас есть две параллельные прямые AB и CD, их пересечение обозначено точкой O. Также у нас есть отрезок BC, который пересекает прямую AD в точке E.
Мы хотим доказать, что точка E принадлежит отрезку AD. Для этого нам необходимо показать, что точка E лежит между A и D. Используя свойство параллельных прямых, мы можем утверждать, что угол AEO равен углу BCO.
Итак, давайте рассмотрим углы внимательнее. Угол AEO - внутренний угол треугольника ADE. Угол BCO - также внутренний угол треугольника DCE. Мы знаем, что углы внутри треугольников всегда суммируются до 180 градусов.
Теперь мы можем сделать вывод, что угол AEO и угол BCO в сумме равны 180 градусов. Но обратите внимание, что угол BCO является частью прямой BCO и поэтому равен 180 градусов. Следовательно, угол AEO также равен 180 градусов.
Когда угол равен 180 градусов, это означает, что его стороны являются продолжениями прямых. То есть, продолжение строится в обратную сторону от угла. В нашем случае, это означает, что прямая AD является продолжением прямой DE.
Теперь мы видим, что точка E лежит на продолжении прямой AD, значит она принадлежит отрезку AD. Доказательство завершено.
Важно отметить, что данное доказательство основано на предположении о том, что прямая AB и прямая CD действительно параллельны. Если бы мы не имели этого предположения, то это доказательство было бы недействительным. Поэтому при решении задачи всегда необходимо учитывать условия и предположения, чтобы убедиться в правильности решения.