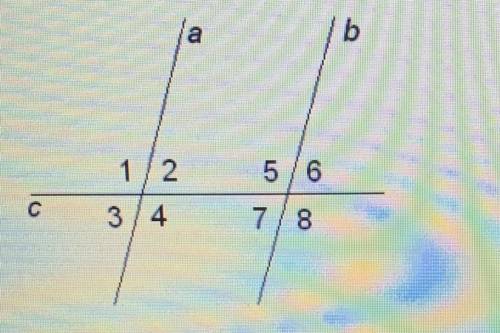
Прямая с пересекает две параллельные прямые а и b.
Отметь, которые из углов равны углу 3.

Добрый день!

Данная задача относится к геометрии и требует нахождения равных углов с использованием свойств параллельных прямых и пересекающей их прямой.

Для начала, обратим внимание на то, что параллельные прямые обозначены латинскими буквами "a" и "b". Также имеется прямая "с", которая пересекает данные параллельные прямые.

Задача заключается в определении, какие углы изображенные на диаграмме равны углу 3. Для этого, нам необходимо обратить внимание на следующие свойства:

1. Параллельные прямые имеют соответственные углы, вершина которых находится на пересекающей их прямой.

Теперь приступим к решению:

1. Обратим внимание на треугольники, образованные параллельными прямыми "a" и "b" с пересекающей их прямой "с".

На диаграмме видно два таких треугольника с вершиной в точке пересечения прямых "а" и "с". Обозначим эти треугольники как "ABC" и "ACD".

[image]

2. Угол 3 в обоих треугольниках имеет общую сторону "AC" и прямую сторону "AD" пересекающую прямую "b". По свойству параллельных прямых, углы "ACD" и "ADH" равны, где "H" - произвольная точка на пересекающей прямой "с".

[image]

3. Также, эти углы равны углам "ABC" и "BCF", так как у них также есть общая сторона "BC" и сторона "BF" пересекает прямую "a". Здесь "F" - еще одна произвольная точка на пересекающей прямой "с".

[image]

4. Следовательно, углы "ACD", "ABC" и "BCF" равны углу 3.

Оставшиеся углы треугольников "ABC" и "ACD", такие как "BAD", "BCD", "CBD" и "DAC", не равны углу 3.

Таким образом, ответ на вопрос состоит в следующем:

Углы, равные углу 3, это углы "ACD" (в треугольнике "ACD"), "ABC" и "BCF" (в треугольнике "ABC").

Надеюсь, ответ был понятным и полным. Если остались какие-либо вопросы, пожалуйста, не стесняйтесь задавать!