Прямая проходит через вершину параллелограмма и делит его площадь в отношении 1:2. В каком отношении эта прямая делит его сторону?

Пусть прямая СЕ проходит через вершину С параллелограмма ABCDE и делит его сторону на отрезки АЕ и ЕD. При этом образуются треугольник ECD и четырехугольник ABCE. Поскольку BC║AE, этот четырехугольник является трапецией.

Пусть АЕ = а, ЕD = b.

Тогда ВС = а + b.

Проведем высоту трапеции к ее основанию a и высоту треугольника к его стороне b.

Эти высоты будут равны, как противоположные стороны образованного прямоугольника.

Чтобы найти площадь треугольника, нужно произведение стороны на высоту, проведенную к ней, разделить пополам.

Значит, .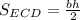

Чтобы найти площадь трапеции, нужно умножить половину суммы ее оснований на высоту.

Значит, .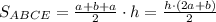

По условию, площади относятся как 1:2.

Отсюда, имеем:

.

По свойству пропорции, произведение ее крайних членов равно произведению средних:

.

ответ: прямая делит сторону параллелограмма в отношении 2:1.