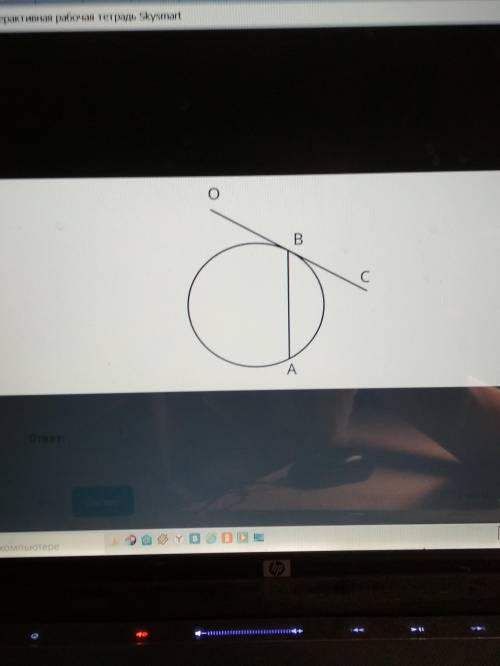
прямая ос касается окружности в точке b найдите величину острого угла ABC если хорда AB разбивает окружность на две дуги в соответствии 2 : 3

72

Объяснение:

.

Для решения данной задачи, нам необходимо использовать некоторые свойства окружности и треугольника.

Обозначим центр окружности как точку O, прямую ось как l, и точки пересечения окружности и прямой оси как B и C.

Из свойства окружности следует, что радиус, проведенный к точке касания, перпендикулярен прямой оси. Таким образом, мы можем заключить, что треугольник OBC является прямоугольным.

Также, из условия задачи мы знаем, что хорда AB разбивает окружность на две дуги в соответствии 2:3. Это означает, что длина одной из дуг в 2 раза больше длины другой дуги. Пусть длина меньшей дуги будет x, а длина большей дуги будет 2x.

Теперь мы можем использовать свойство треугольника, согласно которому угол в прямоугольном треугольнике равен сумме углов, входящих в его острый угол.

Поскольку треугольник OBC прямоугольный, мы знаем, что угол BOC равен 90 градусов.

Также, поскольку AB делит окружность на две дуги, у нас есть оба угла, входящих в острый угол ABC.

Для удобства давайте обозначим точку D на окружности, такую что AD является продолжением AB и делит большую дугу на две равные части. Тогда угол BAC будет равен углу BDC.

Поскольку мы знаем, что большая дуга в 2 раза длиннее меньшей дуги, угол BDC будет в 2 раза больше угла BAC. То есть, угол BDC равен 2x, а угол BAC равен x.

Теперь мы можем найти угол ABC, используя свойство треугольника.

Угол ABC = угол BOC - угол BAC.
Угол ABC = 90 градусов - x.

Таким образом, величина острого угла ABC равна 90 градусов минус x.

Вопрос состоит в том, как найти значение угла x.

Для этого нам необходимо знать какое-то измерение дуги. У нас есть соотношение длин дуг в 2:3, но мы не знаем абсолютные значения этих длин.

Если бы у нас было какое-то измерение, мы могли бы найти значение угла x. Но поскольку мы не имеем информации о размерности дуг, мы не можем точно определить значение угла ABC без дополнительных данных.

В заключение, величина острого угла ABC зависит от отношения длин дуг, но точное значение угла ABC не может быть найдено без дополнительной информации.