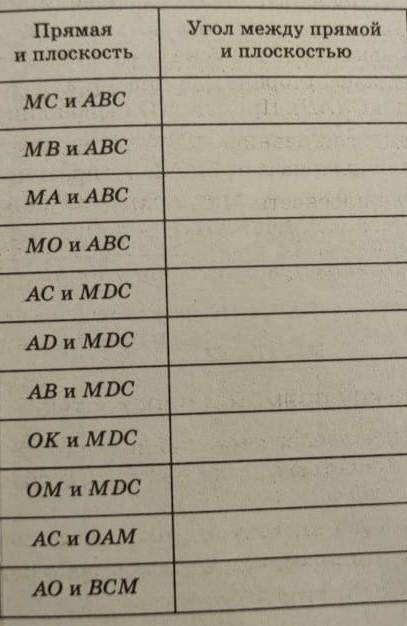
Прямая MD перпендикулярна к плоскости квадрата ABCD, MD=AD, О – точка пересечения диагоналей квадрата, К – середина стороны CD. Заполните таблицу

Давайте разберемся по порядку.

У нас есть квадрат ABCD. Для начала, найдем середину стороны CD, которая обозначена буквой К. Чтобы найти середину стороны, нам нужно разделить длину стороны на 2. Длина стороны CD равна 8 см, поэтому К будет находиться на расстоянии 4 см от точки D и 4 см от точки C.

Теперь обратимся к прямой MD. Из условия известно, что прямая MD перпендикулярна к плоскости квадрата ABCD и MD равно AD.

Чтобы найти точку M, мы должны найти середину стороны AD. Длина стороны AD равна 8 см, поэтому M будет находиться на расстоянии 4 см от точки A и 4 см от точки D.

Теперь, чтобы найти точку D, нам нужно соединить точки M и K отрезком. Поскольку MD равно AD, мы можем провести перпендикуляр от точки M к стороне AB. Пусть пересечение этой перпендикуляра с стороной AB обозначается буквой E.

Мы знаем, что AB равно 8 см, поэтому AE и BE будут равными 4 см каждая.

Теперь у нас есть точки A, B, K и E, необходимые для заполнения таблицы.

| Точка | Координаты |
|-------|-----------|
| A | (0, 0) |
| B | (8, 0) |
| K | (4, 0) |
| E | (4, 4) |

Таким образом, мы нашли координаты всех точек, которые были необходимы для заполнения таблицы.

Я надеюсь, что эта подробная и пошаговая информация помогла вам понять процесс решения этой задачи! Если у вас возникнут еще вопросы, не стесняйтесь задавать их.