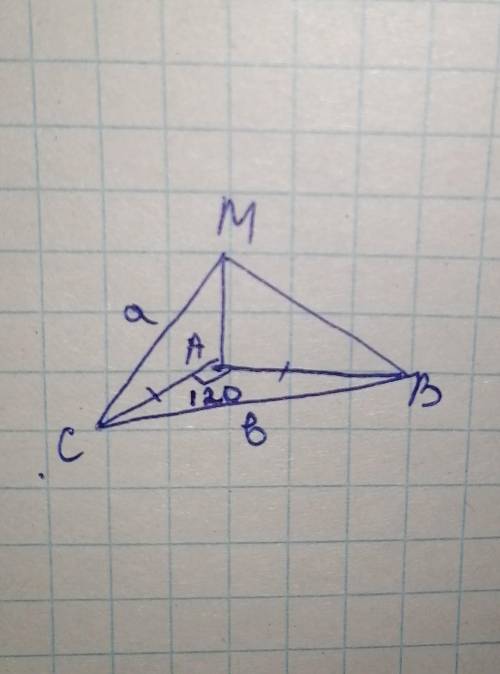
Прямая МА перпендикулярна плоскости АВС. найдите угол между прямой МВ и плоскостью АВС примечание: 120°

Для того, чтобы найти угол между прямой МВ и плоскостью АВС, нам необходимо знать, как взаимодействуют прямая МВ и плоскость АВС. К счастью, у нас есть некоторые данные, которые помогут нам решить эту задачу.

Сначала давайте проанализируем данные. У нас есть прямая МА, которая перпендикулярна плоскости АВС. Это означает, что прямая МА и плоскость АВС пересекаются под прямым углом, то есть наш искомый угол будет 90°.

Теперь нам нужно найти угол между прямой МВ и плоскостью АВС. Угол между двумя линиями или поверхностями можно найти, используя нормали к этим линиям или поверхностям. Нормаль - это вектор, перпендикулярный плоскости или линии.

Поскольку прямая МА перпендикулярна плоскости АВС, вектор, направленный в сторону от точки М к точке А, будет нормалью к плоскости АВС. Обозначим этот вектор как n.

Теперь, чтобы найти угол между прямой МВ и плоскостью АВС, нам нужно найти компоненту вектора n, параллельную прямой МВ. Обозначим эту компоненту как n_parallel.

Так что первым шагом будет найти вектор, направленный от точки М до точки А. Это можно сделать путем вычитания координат точек М и А:

МА = А - М = (х_А - х_М, у_А - у_М, z_А - z_М)

Теперь, используя полученные значения (х_А - х_М, у_А - у_М, z_А - z_М), мы можем построить вектор n, который будет нормалью к плоскости АВС.

Нормализуем этот вектор, чтобы его длина была равна 1:

n_normalized = n / ||n||

Теперь мы можем найти компоненту вектора n_normalized, параллельную прямой МВ, путем скалярного произведения векторов n_normalized и МВ:

n_parallel = n_normalized * МВ = (х_n, у_n, z_n) * (х_В - х_М, у_В - у_М, z_В - z_М) = х_n * (х_В - х_М) + у_n * (у_В - у_М) + z_n * (z_В - z_М)

Наконец, чтобы найти угол между прямой МВ и плоскостью АВС, мы можем использовать следующую формулу:

угол_МВ_и_АВС = arccos(n_parallel / ||МВ||)

где ||МВ|| - длина вектора МВ.

Надеюсь, этот развернутый ответ помог вам понять, как найти угол между прямой МВ и плоскостью АВС. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать!