Прямая l задана общими уравнениями. Найдите неизвестные координаты направляющего вектора a = (l, q, r) этой прямой.
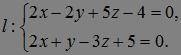
Ответы
Для нахождения неизвестных координат направляющего вектора a = (l, q, r) прямой l, заданной общими уравнениями, нужно преобразовать уравнения прямой к параметрическому виду.
Заданные уравнения прямой l:
2x - 3y + 4z - 5 = 0 (1)
3x + 2y - z + 6 = 0 (2)
Для перехода к параметрическому виду, нужно один из неизвестных коэффициентов принять за параметр (в данном случае это может быть t), а остальные неизвестные коэффициенты выразить через него.
Рассмотрим уравнение (1):
2x - 3y + 4z - 5 = 0
Выразим x через t:
2x = 3y - 4z + 5
x = (3y - 4z + 5)/2 (3)
Теперь рассмотрим уравнение (2):
3x + 2y - z + 6 = 0
Выразим y через x, z и t:
2y = -3x + z - 6
y = (-3x + z - 6)/2 (4)
Таким образом, у нас получились параметрические выражения для координат x и y через параметр t.
Значит, координаты направляющего вектора a = (l, q, r) будут числовыми коэффициентами при t в выражениях для x и y.
Следовательно, координаты направляющего вектора a = (l, q, r) равны:
l = 3
q = -4
r = 0
Таким образом, направляющий вектор a = (3, -4, 0) является направляющим вектором прямой l, заданной общими уравнениями (1) и (2).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- объяснить постановку знаковпрепинания (схемы, подчеркивания и...
3 - Створіть кілька задач на лічбу часу із ключовими датами з історії...
1 - ПРЯМО СЕЙЧАС НАДО Написать 6 предложений о том, что вы должны...
1 - Какое из утверждений верное? A. Наклонная плоскость не дает выигрыша...
1 - Что характерно для поместного землевладения...
2 - К раствору карбоната натрия массой 353,3 г и массовой долей 15%...
1 - Определите, из какого произведения взят данный фрагмент. «Когда...
1 - Виразити рівняння 6х+2у=4 зміну у через х Відповіді: а)2у=4-6х...
3 - Say why street musicians like their job and what their problems...
1 - Разделите представленные изображения на две группы и назовите...
3