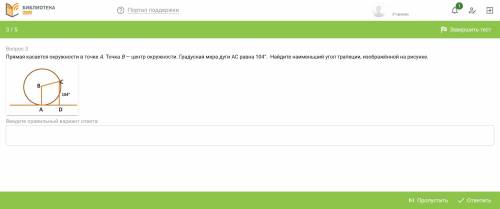
Прямая касается в точку А. Точка B - центр окружности. Градусная мера дуги AC равна 104°. Найдите наименьший угол трапеции, изображенный на рисунке.

Для решения данной задачи нам понадобится использовать знания о свойствах окружности и трапеции. Давайте разберемся пошагово. 1. Заметим, что прямая, проходящая через точку A и центр окружности B, является радиусом окружности. По свойству, радиус, проведенный к точке касания, перпендикулярен касательной в точке касания, то есть к отрезку AC. 2. Так как отрезок AC - дуга окружности, а градусная мера дуги AC равна 104°, то угол, образованный этой дугой, будет равен половине градусной меры дуги, то есть 52°. 3. Из свойств хорд окружности и центрального угла следует, что угол между хордой и касательной, проведенной в точке касания, равен половине центрального угла, образованного этой хордой. Так как хорда AB является основанием трапеции, то у нас есть две хорды AB и AC, образующие один и тот же угол. 4. Значит, угол ABC, образованный хордой AB, будет равен половине угла BAC, то есть половине угла 52°. 5. Получается, что угол ABC равен 26°. Таким образом, наименьший угол трапеции, изображенной на рисунке, равен 26°.