Проверить коллинеарны ли векторы ab и cd. если да, то сонаправлены ди они? a(2; 1), b(-4; 4), c(-1; -1), d(7; -5)

Ответы

Алиса623 22.09.2020 23:43

Чтобы найти координаты вектора, надо вычесть из координат его конца, соответствующие координаты начала.

A(2;1), B(-4;4), C(-1;-1), D(7;-5).

$\vec{AB} =(-4-2;4-1)=(-6;3)\\\\\vec{CD}=(7-(-1);-5-(-1))=(8;-4)$

Векторы коллинеарны, если их соответствующие координаты пропорциональны.

$\dfrac{-6}{8} \; ?\; \dfrac{3}{-4}\\\\-\dfrac34 =-\dfrac34\\\\\vec{AB} \|\vec{CD}$

Если векторы сонаправлены, то их соответствующие координаты имеют одинаковые знаки.

-6<0, однако 8>0. Векторы не сонаправлены, но они коллинеарны. Получается векторы противоположно направлены.

ответ: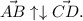 $\vec{AB} \uparrow \downarrow \vec{CD} .$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

xDVadiKSlivE 28.10.2020 09:30

2vovanavi 28.10.2020 09:30

Посогите а то найти ни где не могу...

rodnevadaria 28.10.2020 09:31

Кишинин аскаридасы кайсы ичегиде кездешет?...

арина1253 18.01.2021 20:18

решить) желательно развёрнуто, дам лучший ответ!...

Dimamysixin 18.01.2021 20:18

DashSHAD0W 18.01.2021 20:18

penkoania 18.01.2021 20:16

yashinaalyona20 14.12.2021 06:22

aigerim341 14.12.2021 06:22

Надюфка1997 14.12.2021 06:22