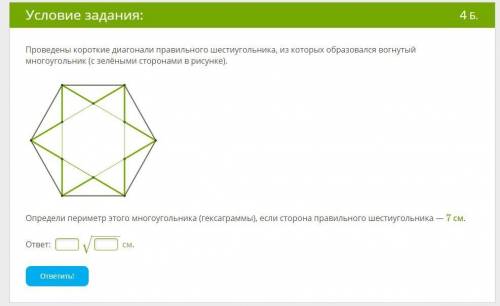
Проведены короткие диагонали правильного шестиугольника, из которых образовался вогнутый многоугольник (с зелёными сторонами в рисунке). Определи периметр этого многоугольника (гексаграммы), если сторона правильного шестиугольника — 7 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- сочинение Как чувства и эмоции влияют на духовный мир человека...
3 - Укажите стилистическую характеристику выделенных слов. Стопроцентно, подчас,...
2 - ответить на эти вопросы! вставить нужное слово...
3 - Всем привет с химией. Нужно составить уравнения реакций согласно схеме превращений....
1 - Что такое буревестник. напишите кластер...
3 - Выбери правильное положение кисти при положение основная стойка ...
1 - подобрать материалы из средств массовой информации или художественной литературы...
2 - расположите в порядке увеличения количества углекислого газа выделяющегося при...
1 - Здравствуйте продаю телефон Huawei P40 Lite EБрала за 90 отдам за 80Телефон цел...
2 - Распределите предложения по группам: «Тире ставится» и «Тире не ставится». Тире...
1
Чтобы решить эту задачу, давайте разобьем гексаграмму на небольшие треугольники и просуммируем длины всех сторон этих треугольников, чтобы найти периметр многоугольника.
Первым шагом, пронумеруем углы гексаграммы следующим образом:
1. Проведем соответствующие вертикали к каждой стороне шестиугольника. Это позволит нам разделить гексаграмму на 6 равносторонних треугольников.
2. Теперь мы можем рассмотреть каждый из этих треугольников.
Треугольник 1: Он образуется из стороны шестиугольника и двух коротких диагоналей.
Так как сторона шестиугольника равна 7 см, стороны треугольника 1 будут иметь длину 7 см.
Треугольник 2: Он образуется из одной стороны шестиугольника и одной короткой диагонали.
Сторона треугольника 2 будет равна стороне шестиугольника, то есть 7 см.
Треугольник 3: Он образуется из одной стороны шестиугольника и одной короткой диагонали.
Сторона треугольника 3 будет равна стороне шестиугольника, то есть 7 см.
Треугольник 4: Он образуется из двух длинных диагоналей.
Чтобы найти длину сторон треугольника 4, нам нужно применить теорему косинусов.
Обозначим длину стороны шестиугольника как 's' и длину одной длинной диагонали как 'd'. Поскольку гексаграмма является правильной, длина каждой стороны шестиугольника равна 's', а длина каждой длинной диагонали равна 'd'.
В треугольнике 4 у нас есть две стороны длинной диагонали (длина 'd') и одна сторона, равная стороне шестиугольника (длина 's'). Угол между этими двумя сторонами равен 60°, так как гексаграмма правильная.
Мы можем использовать теорему косинусов, чтобы найти длину каждой стороны треугольника 4. Формула теоремы косинусов выглядит следующим образом:
c^2 = a^2 + b^2 - 2*a*b*cos(C),
где c - длина стороны, противоположной углу C.
Подставим известные значения в формулу теоремы косинусов.
Пусть a = b = d и C = 60°:
c^2 = d^2 + d^2 - 2*d*d*cos(60°),
c^2 = 2*d^2 - 2*d^2*cos(60°).
c^2 = 2*d^2 - d^2,
c^2 = d^2.
Это означает, что длина каждой стороны треугольника 4 равна длине длинной диагонали, то есть 'd'.
Таким образом, сторона треугольника 4 будет равна длине длинной диагонали, а значит, равна 'd', которую мы пока не знаем.
Треугольники 5 и 6: Они также образуются из стороны шестиугольника и короткой диагонали.
Степень острых углов в треугольниках 5 и 6 может быть найдена по теореме косинусов, как в треугольнике 4. Мы можем использовать эту степень для нахождения длины стороны каждого из этих треугольников.
Таким образом, периметр гексаграммы будет равен сумме длин всех шести сторон треугольников 1-6. Давайте найдем эти значения:
Периметр гексаграммы = (7 + 7 + 7 + d + d + 7 + 7 + d + 7 + 7 + 7).
Теперь нам нужно найти значение 'd'. Обратимся к треугольнику 5. Мы можем использовать теорему косинусов с длиной стороны, равной 's' и степенью острого угла в 120° (треугольник 5), чтобы найти длину диагонали 'd'.
Пусть a = b = s и C = 120°:
d^2 = s^2 + s^2 - 2*s*s*cos(120°),
d^2 = 2*s^2 - 2*s^2*cos(120°),
d^2 = 2*s^2 - s^2,
d^2 = s^2.
Это означает, что длина стороны треугольника 5 равна длине длинной диагонали, то есть 'd'.
Теперь мы можем подставить это значение 'd' в периметр гексаграммы:
Периметр гексаграммы = (7 + 7 + 7 + d + d + 7 + 7 + d + 7 + 7 + 7),
Периметр гексаграммы = (7 + 7 + 7 + d + d + 7 + 7 + d + 7 + 7 + 7),
Периметр гексаграммы = (7 + 7 + 7 + d + d + 7 + 7 + d + 7 + 7 + 7),
Периметр гексаграммы = (35 + 4d).
Теперь нам нужно найти значение 'd', чтобы решить эту задачу окончательно. Снова обратимся к треугольнику 5, где сторона равна 7 см.
d^2 = 7^2,
d^2 = 49,
d = √49,
d = 7.
Теперь мы можем подставить это значение 'd' в периметр гексаграммы:
Периметр гексаграммы = (35 + 4 * 7),
Периметр гексаграммы = (35 + 28),
Периметр гексаграммы = 63 см.
Итак, периметр этого многоугольника (гексаграммы) составляет 63 см.