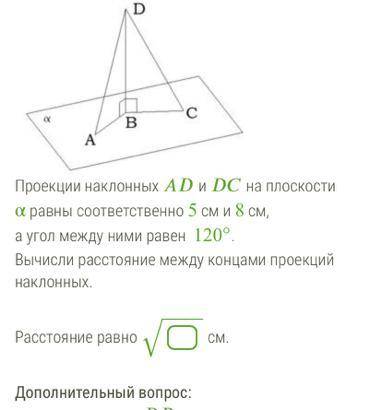
Проекции наклонных и на плоскости α равны соответственно 5 см и 8 см, а угол между ними равен 120°.
Вычисли расстояние между концами проекций наклонных.
Расстояние равно ‾‾‾‾‾√ см.
Дополнительный вопрос:
название отрезка —
Другие вопросы по теме Геометрия
Популярные вопросы
- Нам по изо (изобразительное искусство, рисование) задали написать...
2 - Составьте схемы этих предложений, , ...
3 - Какие факторы влияют на выбор профессии?...
1 - Nbsp; число электронов внешнего уровня увеличивается в ряду элементов:...
3 - Декодируйте следующий текст, заданный десятичным кодом: 087 111...
1 - Сдерева выбора и таблицы джо гарпер начал решать такую...
2 - Які з пар чисел с розв язком рівняння з двомазмінними зr - 2y =...
3 - Nh3++h2o n2+o2--no h2s+ +so2 so2+kr2++hbr ae+(so4)+h2(выпадает...
3 - Сделать синтаксический разбор и схему предложения ( 2 придложений)...
2 - Какова нормальность 4m серной кислоты?...
1
Начнем с того, что построим треугольник ABC, где А и В - концы проекций наклонных, а С - точка, где проекции пересекаются.
Теперь нам известны значения сторон треугольника AB и AC: АВ = 5 см и АС = 8 см. Для того чтобы найти расстояние между концами проекций наклонных (т.е. сторону ВС), нам понадобится использовать теорему Пифагора.
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, гипотенузой является сторона AC, а катетами – AB и BC.
Итак, у нас есть следующее уравнение:
AC² = AB² + BC²
Подставляем известные значения:
8² = 5² + BC²
Решаем это уравнение:
BC² = 8² - 5²
BC² = 64 - 25
BC² = 39
Для того чтобы найти значение BC, мы извлекаем квадратный корень из 39:
BC = √39
Итак, расстояние между концами проекций наклонных равно √39 см.
Ответ на дополнительный вопрос: Название отрезка, который соединяет концы проекций наклонных, может быть обозначено как BC.