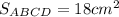Продовження бічних сторін АВ і CD трапеції ABCD перетинаються в точці М. Знайдіть площу трапеції, якщо ВС:AD = 2:5, а площа трикутника ВМС дорівнює 12 см² ???
Другие вопросы по теме Геометрия
Популярные вопросы
- Составьте рассказ об одном из следующих событий от имени его участника:...
3 - Вызначце галоўную прычыну паўстання пад кіраўніцтвам Спартака і...
2 - У кого выступление Тиберия могло вызвать ненависть?...
2 - Каким было положение римских рабов? Что общего вы можете отметить...
3 - Складзіце паведамленне аб адным з наступных падзей ад імя яго ўдзельніка:...
1 - Определите главную причину восстания под предводительством Спартака...
2 - Мирились ли рабы со своей участью? Как вы считаете, почему самых...
2 - Опишите вторую Пуническую войну: а) от имени Ганнибала; б) от имени...
1 - Пералічыце крыніцы рабства ў Старажытным Рыме...
2 - Перечислите источники рабства в Древнем Риме...
1
Дано:
Розв'язання:
1) Якщо провести відрізки BM та CM, то утворяться два подібні трикутники BMC та AMC за двома кутами (кут М - спільний, а кут D = куту MCB, бо кут BCD + кут D = кут BCD + кут MCB = 180). У подібних трикутниках відношення сторін дорівнює відношенню площ.
2)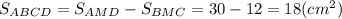
Відповідь: