Продолжаю раздачу . На кону максимум )) Есть две одинаковые сферы, объем каждой .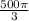
Расстояние между их центрами равно 10.
Найти объем фигуры, образованной пересечением этих сфер.

Задача может показаться сложной только на первый взгляд ;)
Гуру не участвовать.
Лучшим ответом сделаю ответ участника с наименьшим количеством количеством и наименьшим статусом.
Как обычно за спам - бан и минус .
Вперед!

V=0.

Пересечением двух сфер является точка, т.е.

взаимное расположение сфер таково, что

они касаются.

Объяснение:

V=4/3piR^3

По условию V=500pi/3 ,

следовательно: 4/3рiR^3=500pi/3

4R^3=500

R^3=125

R=5.

Расстоянме между центрами сфер :

5+5=10 - сферы не пересекаются, а имеют

лишь точку внешнего касания.

Две сферы.

V = 500п/3 ед. кб.

d = 10 ед.

V - ?

R1 - радиус первой сферы.

R2 - радиус второй сферы.

Составим уравнение, с которого узнаем, чему равен радиус R1

Пусть х - радиус R1

V сферы = 4/3пR^3 = 500п/3

В уравнении число п нам не нужно, так как при вычислении объёма сферы, видео, что число п не вычислялось:

4/3 * х^3 = 500/3

х^3 = 125

х^3 = 5^3

х = 5

Итак, R = 5 см

Так как d = 10 см => R1 = R2 = 5 см, так как R1 + R2 = 5 + 5 = 10 см

Из этого =>, что две сферы касаются внешним образом.

=> сферы образуют одну общую точку, но они не образуют никакой фигуры, то есть V = 0