Признаки подобия треугольников
Найти Х,У.
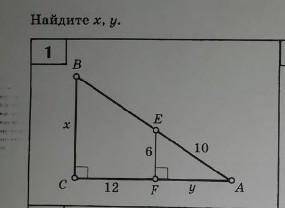
Другие вопросы по теме Геометрия
Популярные вопросы
- 7. Рухани байлықтың түрін көрсет А) киім-кешек В) тамақ С) кітап 9. Болжалдық...
2 - Alex is taller than Sam.Alex is shorter and younger than Ben.Sam is younger than...
1 - Для того чтобы посеребрить медное изделие массой 24г, содержащее 40% примесей,...
3 - 3. Дополните рисунок – схему....
1 - Выберите одно из 3-х высказываний и напишите эссе, опираясь на тексты произведений...
1 - Запишите все целые числа, расположенные на координат ной прямой между числами...
3 - Напишите краткий пересказ книги horse whisperer на английском...
2 - 1 км2 территориядағы адам саны қалай аталады?...
3 - Кекілік диктантының сын есімдері...
2 - ФИЗИКА ТЖБ 7 СЫНЫП 1 ТОҚСАН...
1
Для начала, нам нужно понять, какие признаки подобия треугольников существуют.
1. Первый признак подобия треугольников - это угловой признак. Если все углы одного треугольника равны (то есть треугольник прямоугольный, равнобедренный, равносторонний или просто все его углы равны), то он подобен треугольнику с такими же углами.
2. Второй признак подобия треугольников - это соотношение длин сторон треугольников. Если для двух треугольников отношение длин их соответствующих сторон равно, то они подобны.
Теперь давайте решим задачу.
У нас есть два треугольника - АВС и МНК. Нам нужно найти значения Х и У.
Сначала посмотрим на угловые признаки треугольников. В треугольнике АВС мы видим, что угол А равен 90 градусов, а угол С равен 35 градусов. В треугольнике МНК угол М равен 90 градусов, а угол К равен 30 градусов. Мы видим, что оба треугольника имеют один прямой угол, поэтому угловой признак выполнен.
Теперь посмотрим на соотношение сторон треугольников.
Для этого воспользуемся третьим признаком подобия треугольников - это соотношение длин сторон.
Мы видим, что сторона АВ в треугольнике АВС равна 4 см, а сторона МН в треугольнике МНК равна 6 см.
Стороны ВС и НК в наших треугольниках нам не даны, поэтому нам нужно использовать другие стороны для определения подобия треугольников.
Обратимся к сторонам АС и МК.
У нас есть отношение 2:3, поэтому можно сделать вывод, что отношение длин сторон треугольников АВС и МНК равно 2:3.
Теперь, когда мы установили, что треугольники подобны по угловому признаку и отношению длин сторон, мы можем перейти к нахождению значений Х и У.
У нас есть сторона ВС в треугольнике АВС, которая равна 6 см. Мы можем найти отношение сторон треугольников АВС и МНК:
4/6 = 2/Х.
Мы можем решить эту пропорцию:
4Х = 6*2.
4Х = 12.
Х = 12/4.
Х = 3.
Таким образом, Х равно 3.
Теперь давайте найдем значение У. У нас есть сторона АС в треугольнике АВС, которая равна 4 см.
Мы можем использовать отношение сторон треугольников:
4/6 = У/4.
Мы можем решить эту пропорцию:
4У = 6*4.
4У = 24.
У = 24/4.
У = 6.
Таким образом, У равно 6.
Итак, мы нашли значения Х и У. Х равно 3, а У равно 6.