Признак подобия треугольника
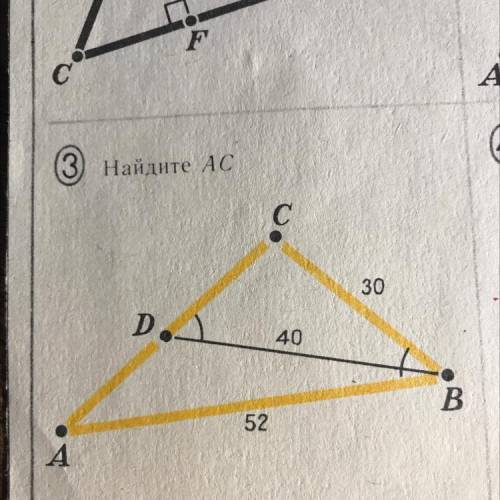
Найдите АС
Если АВ-52, ДВ-40, СВ-30

Для нахождения длины стороны АС в треугольнике, мы можем использовать теорему подобия треугольников.

Теорема гласит, что если два треугольника подобны, то отношение длин соответствующих сторон равно отношению длин соответствующих сторон в другом треугольнике.

В данном случае мы знаем отношение длин сторон АВ, ДВ и СВ, исходя из этой информации мы можем найти длину стороны АС.

Поскольку мы знаем, что треугольник АВС подобен треугольнику ДВС, можно записать отношение длин сторон:

(АВ / ДВ) = (СВ / СД)

Заменим известные значения:

(52 / 40) = (30 / СД)

Мы можем найти СД, перекрестием произведение значений на одну сторону и делением на другую:

52 * СД = 40 * 30

Рассчитаем произведение:

СД = (40 * 30) / 52

СД = 1200 / 52

СД ≈ 23.08

Таким образом, мы нашли длину стороны СД, которая равна приблизительно 23.08.

Ответ: длина стороны АС признака подобия треугольника равна приблизительно 23.08.