Привет, трудности с геометрией решить, только не копируйте ниоткуда... ;-; Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен 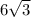 см. Найдите стороны треугольника
см. Найдите стороны треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- 21. Позначте групу рослин, у яких плід - кістянка: * малина, глід, персик...
2 - Тест. Выбери из предложенного списка то, что характеризует товарищество....
2 - Численність населення країни на 1 січня 2010 року становила 100млн....
2 - Три резистора R1, R2 та R3 з єднані послідовно . Визначити величину...
1 - Два прямоугольника имеют одинаковую площадь. Длина первого прямоугольника...
1 - 1. Как образование факультативного гетерохроматина повлияет на проявление...
3 - надо : Напишите значение следуйших слов: Раскалённый Горизонт...
2 - Какой вид омонимов представлен в примере: пушистая НОРКА – глубокая...
1 - Основою прямої призми е паралелограм зі сторонами 3/2 см i v2 см і кутом...
1 - Потрібно скласти план профілактичних заходів попередження і передачі...
2
Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника
Объяснение:
ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.
Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.
По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) :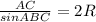 ,
, 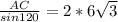 , АС=12√3*
, АС=12√3*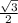 =18 (см).
=18 (см).
По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.
ΔАВН-прямоугольный , sin 60°=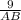 , АВ=6√3 см ⇒ВС=6√3 см.
, АВ=6√3 см ⇒ВС=6√3 см.