1. Геометрия
  2. Прикрепите ! высота правильной

Прикрепите !

высота правильной четырехугольной призмы равна 18 см, а диагональ призмы образует с плоскостью ее основания угол 60 °. найдите сторону основания призмы и угол, который диагональ призмы образует с ее боковой гранью.

ololoololoev1 ololoololoev1    3   22.09.2019 19:02    59

Ответы
Космос1986 Космос1986  08.10.2020 10:19

AD=\frac{18}{\sqrt{6}}

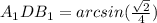
∠A_{1}DB_{1} = arcsin(\frac{\sqrt{2} }{4})

Объяснение:

Призма ABCDA₁B₁C₁D₁, ∠B₁DB=60°, BB₁=18см. AD=? ∠A₁DB₁=?

1) Правильная четырехугольная призма => ABCD - квадрат, BB₁D - прямоугольный треугольник (∠DBB₁=90°)

ABCD - квадрат => В ΔABD ∠DAB=90° =>BD²=AD²+AB²

AD=AB=A₁B₁=x, BD=y, B₁D=z =>

x^{2} +x^{2} =y^{2} = 2x^{2} =y^{2} = y=x\sqrt{5} = x=\frac{y}{\sqrt{2} } \\cosB_{1} DB=\frac{BD}{B_{1} D} =\frac{y}{z} = \frac{y}{z} =cos(60^{o} )=\frac{1}{2} = y=\frac{z}{2} \\sinB_{1} DB=\frac{BB_{1}}{B_{1} D} =\frac{18}{z} = \frac{18}{z} =sin(60^{o} )=\frac{\sqrt{3} }{2} = z=\frac{18*2}{\sqrt{3} } \\=y=\frac{18*2}{2\sqrt{3} } =\frac{18}{\sqrt{3} }\\= x=\frac{18}{\sqrt{3}*\sqrt{2}}=\frac{18}{\sqrt{6}}

2) Угол между диагональю и гранью  - угол между диагональю и её проекцией на эту грань. A₁D - проекция диагонали B₁D на AA₁D₁D => нужно найти ∠A₁DB₁

Правильная четырехугольная призма =>A₁B₁ ⊥AA₁D₁D => В ΔA₁B₁D ∠B₁A₁D=90° =>

sinA_{1} DB_{1} =\frac{A_{1}B_{1}}{B_{1}D} =\frac{x}{z} =\frac{18}{\sqrt{6} * \frac{\sqrt{3} }{18*2} } =\frac{1}{2\sqrt{2} } =\frac{\sqrt{2} }{4} = A_{1} DB_{1} =arcsin(\frac{\sqrt{2} }{4})


Прикрепите ! высота правильной четырехугольной призмы равна 18 см, а диагональ призмы образует с пло
Прикрепите ! высота правильной четырехугольной призмы равна 18 см, а диагональ призмы образует с пло
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Препод007 Препод007  08.06.2021 13:14
Cos x меньше или равен 0 ​...
Lizavladimir07 Lizavladimir07  04.06.2019 16:50
Впрямоугольных треугольниках авс и хту равны катеты ав и хт; вс и ту.обязательно ли эти треугольники равны,и почему?...
nikita540601 nikita540601  01.07.2019 21:40
Вокружность диаметром 10 см вписан равнобедренный треугольник с высотой пробеденной к основанию. найдите основания треугольника если высота равна 2 см...
ТаняСажнева486 ТаняСажнева486  01.07.2019 21:40
Впрямоугольном треугольнике авс с прямым углом с и катетом вс = 9 радиус вписанной окружности равен 3. найти: а) стороны ав и ас; б) расстояние между центрами вписанной и...
anyta03 anyta03  01.07.2019 21:40
Треугольник abc равнобедренный,ac=bc= 8sqrt{6} cм угол c= 90^{0} плоскость a проходит через сторону ac причем сторона ab образует с плоскостью a угол 30^{0} найдите расстояние...
елена13333 елена13333  01.07.2019 21:40
Найдите площадь квадрата,сторона которого равна стороне ромба с диагоналями 40 и 30...
565п 565п  23.04.2019 23:10
Основания трапеции равны 12 и 44. найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей...
qwrt1337 qwrt1337  23.04.2019 23:10
Высота прямоугольного треугольника, проведённая из прямого угла, равна 5 см, один из катетов равен 13 см. найдите гипотенузу....
RengevychPolina RengevychPolina  23.04.2019 23:10
Какая фигура образуется при вращении треугольника авс вокруг оси. вычислите полную поверхность тела которое получается в результате вращения треугольника авс вокруг его стороны...
kristinaboss15 kristinaboss15  23.04.2019 23:10
Сторона ав квадрата авсd, равная 13 см, лежит в плоскости. расстояние от прямой сd до этой плоскости 2 см. найдите расстояние от основания перпендикуляра, опущенного из точки...

Популярные вопросы