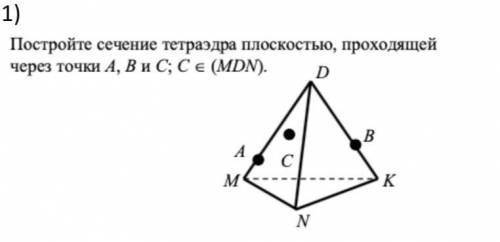
Постройте сечение тетраэдра плоскостью, проходящей через точки A, B и C, C принадлежит (MDN) (пошагово, с объяснением)

Для построения сечения тетраэдра плоскостью, проходящей через точки A, B и C, и где C принадлежит (MDN), следуйте следующим шагам:

Шаг 1: Нарисуйте тетраэдр ABCD, где A, B, C и D образуют его вершины. Обозначим стороны как AB, AC, AD, BC, BD и CD.

Шаг 2: Проведите отрезок MD, который будет пересекать грань ABCD и проходить через точки M и N, так как C находится на (MDN). Отметьте точки M и N на отрезке CD.

Шаг 3: Проведите отрезки AM и BN, соединяющие вершины A и M, и B и N соответственно.

Шаг 4: Проведите отрезок CM, соединяющий точки C и M. Поскольку сечение проходит через точки A, B и C, плоскость должна пересекать эти отрезки.

Шаг 5: Проведите отрезок CN, соединяющий точки C и N.

Шаг 6: Проведите плоскость, параллельную плоскости ABC и проходящую через отрезки CM и CN. Эта плоскость будет сечением тетраэдра.

Шаг 7: Отметьте точки пересечения плоскости и отрезков AM и BN. Обозначьте эти точки как E и F соответственно.

Шаг 8: Проведите отрезки CE, AE, CF и BF, соединяющие вершины C и E, A и E, C и F, B и F соответственно.

Шаг 9: Отрезки CE и AE будут пересекаться с отрезками CM и AM соответственно, а отрезки CF и BF будут пересекаться с отрезками CN и BN соответственно. Пометьте точки пересечения отрезков как H, G, I и J соответственно.

Шаг 10: Проведите отрезки EH, GH, FI и JI, соединяющие точки E и H, G и H, F и I, J и I соответственно.

Шаг 11: Отрезки EH и GH будут пересекаться с отрезками AB и CD соответственно, а отрезки FI и JI будут пересекаться с отрезками AD и BC соответственно. Пометьте точки пересечения отрезков точками K, L, O и P соответственно.

Шаг 12: Проведите отрезки KL, PL, OL и KO, соединяющие вершины K и L, P и L, O и L, K и O соответственно.

Шаг 13: Отрезки KL, PL, OL и KO будут пересекать другие отрезки соответствующих граней тетраэдра ABCD. Пометьте точки пересечения отрезков как точки Q, R, S и T соответственно.

Шаг 14: Постройте четырехугольник KQRS, соединяющий точки K, Q, R и S. Этот четырехугольник будет сечением тетраэдра плоскостью, проходящей через точки A, B и C, где C принадлежит отрезку MDN.

Таким образом, сечение тетраэдра плоскостью, проходящей через точки A, B и C, где C принадлежит (MDN), будет представлять собой четырехугольник KQRS.