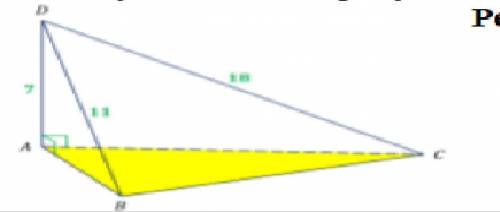
Пользуясь данными рисунка, определите расстояние от точки D до плоскости ABC. AD=7см, DB=11см, DC=18см
Решение

Добрый день! Давайте решим эту задачу вместе.

В задаче нам нужно найти расстояние от точки D до плоскости ABC, учитывая данные рисунка и длины отрезков AD, DB и DC.

Давайте вначале рассмотрим подход к решению. Поскольку задача связана с построением расстояния от точки до плоскости, мы можем использовать формулу для нахождения расстояния между точкой и плоскостью.

Итак, давайте определим расстояние от точки D до плоскости ABC. Мы можем использовать формулу:

Расстояние = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)

где (x, y, z) - координаты точки D, A, B, C и D - параметры плоскости ABC.

Для начала нам нужно определить параметры плоскости ABC. Мы знаем точки A, B, C, поэтому мы можем найти параметры плоскости, используя метод векторного произведения и координаты этих точек.

После того как мы определили параметры плоскости ABC, мы можем перейти к определению координат точки D. Мы знаем длины отрезков AD, DB и DC, но нам нужно найти конкретные координаты точки D. Для этого мы можем воспользоваться методом пропорции, чтобы найти относительные координаты точки D относительно точек A, B и C. Затем мы можем использовать координаты этих точек и параметры плоскости ABC для подстановки в формулу и нахождения расстояния от точки D до плоскости ABC.

Таким образом, мы можем приступить к решению задачи, используя пошаговый подход. Я направлю вас через каждый из этих шагов для полного понимания решения задачи.