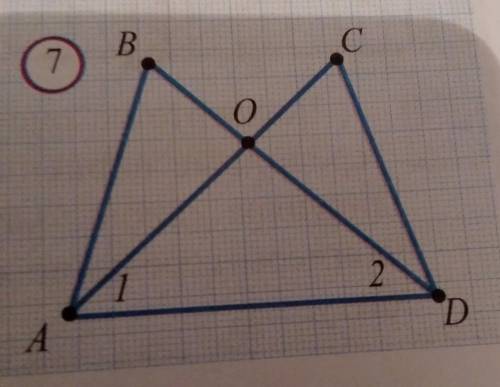
покажите что на рисунке 7 выполняется равенство: ABD=DCA,если а) угол 1= углу 2, AC=BD; б) угол 1 =угол 2, BO=OC, AB=CD​

Добрый день!

Для доказательства равенства ABD = DCA на рисунке 7, воспользуемся данной информацией:

а) Если угол 1 равен углу 2 и AC равно BD.

1. Рассмотрим треугольник ABC и треугольник CDA. У нас есть две известные информации: угол 1 равен углу 2 и AC равно BD.
2. Углы, лежащие на одном луче, которые равны друг другу, называются вертикальными углами. Таким образом, угол ABC равен углу ADC из-за данного условия.
3. Когда два угла в одном треугольнике равны двум углам в другом треугольнике, то такие треугольники называются равными по 3 углам. Значит, треугольник ABC равен треугольнику ADC.
4. По определению, равные двум прямым треугольникам равны и соответствующие стороны. Так как AC равно BD, то AB равно CD, и соответствующие стороны треугольников ABC и CDA равны.
5. Таким образом, мы доказали, что угол ABD равен углу DCA, если угол 1 равен углу 2 и AC равно BD.

б) Если угол 1 равен углу 2, BO равно OC и AB равно CD.

1. Рассмотрим треугольник ABC и треугольник CDA. У нас есть три известные информации: угол 1 равен углу 2, BO равно OC и AB равно CD.
2. Углы, лежащие на одном луче, которые равны друг другу, называются вертикальными углами. Таким образом, угол ABC равен углу ADC из-за данного условия.
3. Когда два угла в одном треугольнике равны двум углам в другом треугольнике, то такие треугольники называются равными по 3 углам. Значит, треугольник ABC равен треугольнику ADC.
4. По определению, равные двум прямым треугольникам равны и соответствующие стороны. Так как AB равно CD, то AC равно BD, так как BO равно OC. Следовательно, соответствующие стороны треугольников ABC и CDA равны.
5. Таким образом, мы доказали, что угол ABD равен углу DCA, если угол 1 равен углу 2, BO равно OC и AB равно CD.

Таким образом, независимо от условий, мы доказали, что угол ABD равен углу DCA на рисунке 7.