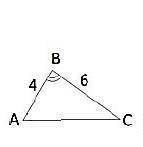
Покажите, что два треугольника на рисунке ниже являются подобными​

Чтобы показать, что два треугольника являются подобными, нужно установить, что у них соответствующие углы равны, а соответствующие стороны пропорциональны.

На рисунке ниже представлены два треугольника: ABC и DEF.
Треугольник ABC имеет стороны AB, BC и AC, а треугольник DEF имеет стороны DE, EF и DF.

Для начала, рассмотрим соответствующие углы треугольников ABC и DEF.
Угол A соответствует углу D, угол C соответствует углу F.

Теперь, нужно показать, что стороны треугольников также пропорциональны.
Рассмотрим отношение сторон:
AB/DE = BC/EF = AC/DF

Чтобы понять, какие стороны относятся друг к другу, рассмотрим длины сторон на рисунке:

AB = 4 см, BC = 5 см, AC = 6 см
DE = 2 см, EF = 2.5 см, DF = 3 см

Подставим значения в соотношение:
4/2 = 5/2.5 = 6/3

Приведем значения к наименьшему общему знаменателю:
2/1 = 2/1 = 2/1

Таким образом, получили, что отношение сторон для треугольников ABC и DEF равно 2/1 для всех трех соотношений.

Следовательно, можем сделать вывод, что два треугольника ABC и DEF являются подобными, так как соответствующие углы равны, а соотношение сторон одинаковое.

С уважением, ваш учитель.