ПОИОГИТЕ ЗАДАНИЕ ПО ГИОМЕРТИИ(если можно пришлите фото )

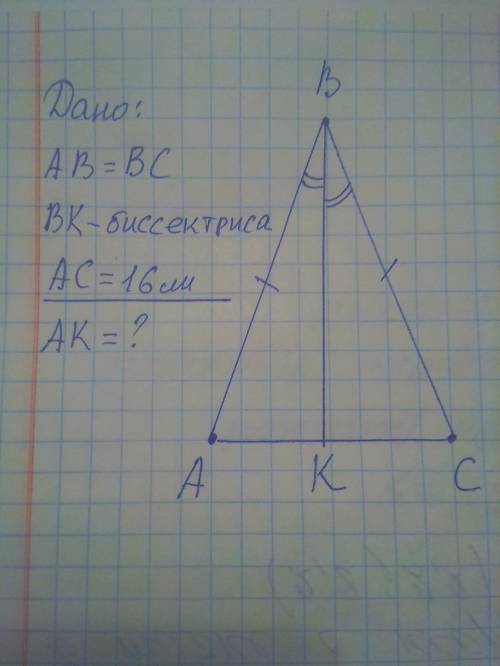
Решение к первому фото:

Т.к., по условию, AB = BC, то /\ ABC - равнобедренный с основанием AC. Как известно, биссектриса, проведённая в равнобедренном трегольнике к основанию - это и медиана, и высота => AK = KC. Зная, что AC = 16 см и то, что BK - медиана, находим AK : 16÷2 = 8 см.

ответ : 8 см

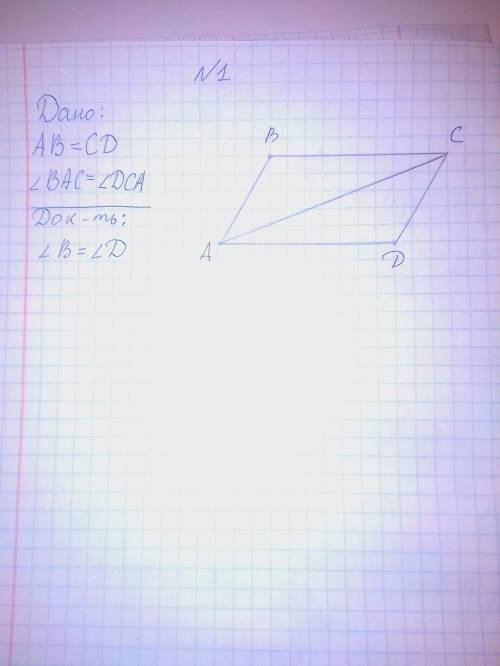
Решение ко второму фото :

Докажем, что /\ ABC = /\ ADC. По условию, AB = CD, а угол BAC = углу DCA. Также, сторона AC - общая => /\ ABC = /\ ADC по 1 признаку => угол B = углу D, ч.т.д.

8

Объяснение:

По условию в треугольнике АВС АВ=ВС => треугольник АВС равнобедренный, где ВК бисситриса => по свойству равнобедренного треугольника ВК медиана=> АК=АС => ВК= 2АК Или АК= 16÷2=8