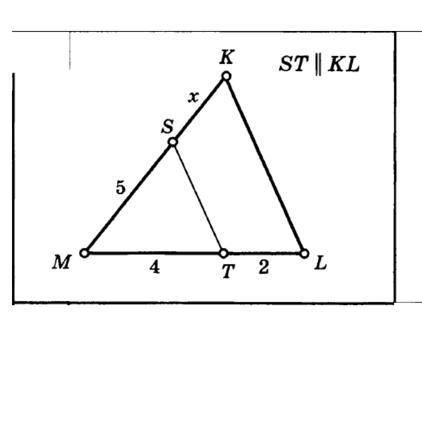
Подобные треугольники с задачей
Другие вопросы по теме Геометрия
Популярные вопросы
- Як зміниться сторона квадрата, якщо його площу: 1) збільшити у...
2 - Впервый день в магазине продали 69кг овощей,что составляет три...
2 - Какое травянистое растение растёт в лесу? тимофеевка, вороний...
1 - Самолет массой 150 т. имеет скорость 288 км/ч в момент отрыва...
1 - Хватит ли 15 литров кислорода для сжигания 4 граммов серы...
2 - мне нужно составить не большой доклад по физ-ре. техника безопасности...
2 - Сочинение 12-15 предложений почему мы должны учить язык?...
3 - Масса 15 см кубических некоторого вещества равна 109,5 г. какое...
3 - Какая функция является ни чётной, ни нечётной? объясните, ....
2 - Вкаких порциях веществ содержится больше молекул (объемы газов...
3
У нас есть два треугольника: большой треугольник АВС и маленький треугольник ХYZ. Размеры треугольников даны следующим образом:
АВ = 4, ВС = 6, АС = 10, УХ = 2, УZ = ?.
Мы хотим найти значение УZ, то есть длину отрезка УZ. Для решения этой задачи мы можем использовать свойство подобия треугольников.
Два треугольника называются подобными, если их соответствующие углы равны, и их соответствующие стороны пропорциональны. Из данной задачи мы можем сделать предположение, что треугольники АВС и ХYZ подобны.
Теперь мы можем сформулировать отношение между сторонами треугольников АВС и ХYZ. В данной задаче мы знаем, что сторона АВ равна 4, а сторона ХУ равна 2. Мы также знаем, что сторона АС равна 10, и мы хотим найти сторону УZ.
Мы можем записать отношение между сторонами следующим образом:
АВ/ХУ = АС/УZ.
Теперь мы можем записать известные значения:
4/2 = 10/УZ.
Мы можем упростить это уравнение, умножив обе стороны на УZ и делением на 2:
(4 * УZ)/(2 * 1) = (10 * 1)/(1 * 1).
Теперь мы можем упростить это дальше:
(2 * УZ) = 10.
Чтобы найти УZ, мы делим обе стороны на 2:
УZ = 10 / 2.
Теперь мы можем выполнить эту операцию:
УZ = 5.
Таким образом, длина отрезка УZ равна 5.
Итак, мы решили задачу, используя подобие треугольников и решая уравнение с помощью пропорций. Длина отрезка УZ равна 5.