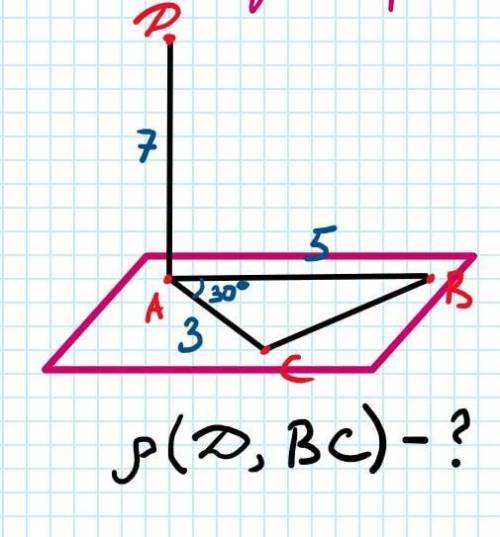
по теореме трёх перпендикуляров. Прямая DA перпендикулярная плоскости альфа (в плоскости лежит треугольник ABC) и касается точки А. AC = 3 см. AB = 5 см. Угол BAC = 30 градусов. DA = 7 см. Найти расстояние от точки D до BC в см.
Другие вопросы по теме Геометрия
Популярные вопросы
- В каком равновесии находится канатоходец?...
2 - Можно ли натянуть веревку горизонтально так, чтобы она не провисала?...
3 - Две параллельные силы действуют на тело в точках А и В. Изменится ли величина и...
2 - Почему продукты легче резать не просто надавливая на нож, а надавливая и двигая...
3 - При торможении вагона троллейбуса, поезда метро и т. п. наблюдается следующее явление:...
3 - Что произойдет, если, сидя в лодке, двигать веслами в противоположные стороны?...
3 - Стержень из проволоки подвешен на нити за середину. Останется ли он в равновесии,...
3 - На веревочной петле в горизонтальном положении висит палка. Один конец палки значительно...
2 - В каких видах равновесия может быть шар на горизонтальной плоскости, если одна...
2 - С какой целью цирковые артисты при хождении по канату держат в руках тяжелые шесты?...
2
DM≈7см
Решение:
S(∆ABC)=½*AC*AB*sinCAB
sin30°=1/2
S(∆ABC)=½*3*5*½=3,75см²
Теорема косинусов
СВ=√(АС²+АВ²-2*АС*АВ*cosCAB)
cos30°=√3/2
CB=√(5²+3²-2*5*3*√3/2)=
=√(25+9-15√3)=√(25+9-26)≈√8≈3.
S(∆ABC)=½*AM*CB;
AM=2*S(∆ABC)/CB=2*3,75/3=7,5/3=
=2,5см
∆DAM- прямоугольный треугольник
По теореме Пифагора
DM=√(DA²+AM²)=√(7²+2,5²)=
=√(49+6,25)=√55,25≈7см