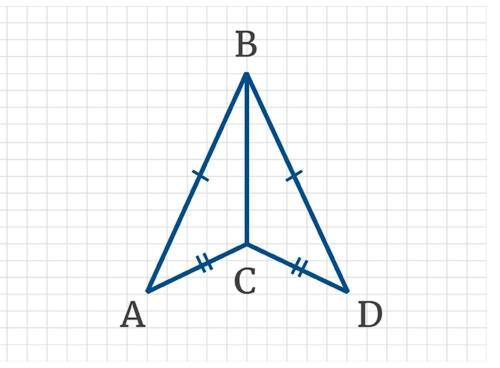
По рисунку найдите градусную меру угла ABD, если угол ABC равен 30°

Алтын сақаның бас қаһарманы, идеялық нысанасы - халықтың арман-мұраты. Мұнда да халықтың аңсары ертегінің басты арқауы. Қазақ ертегілерінің бас қаһармандары аңшы-мерген, жауынгер-батыр, кенже бала, тазша бала, жалғыз бала және басқа әлеуметтік теңсіздіктегі бұқара өкілі. Бұлардың бәрі - халық арманынан әр кезде туған идеал кейіпкерлер. «Алтын сақадағы» бала сондай кейіпкер. Онда классикалық батырлық ертегіге тән белгілердің бәрі бар. Бала жұртта қалып қойған алтын сақасын алып келуге барып, жалмауыз кемпірге кез болған бала кемпірдің алдағанына сенбей, сақасын ат үстінен іліп алып, қаша жөнеледі. Мыстан кемпір тұра қуады. Осымен оқиға шиеленісе түседі. Бұл ертегіде де сайыста кейіпкер өз күшімен емес, керемет достарының арқасында жеңуі - батырлықтан гөрі қиял-ғажайып ертегінің заңдылықтарына жақындау.

Для решения этой задачи мы можем использовать свойство суммы углов треугольника.
1. Начнем с рассмотрения треугольника ABC. Мы знаем, что градусная мера угла ABC равна 30°.
2. Так как сумма всех углов треугольника равна 180°, мы можем вычислить, что градусная мера угла BAC равна 180° - 30° - 80° = 70°.
3. Посмотрим на треугольник ABD. У нас уже есть информация о градусной мере угла BAD, которая равна 80°.
4. Используя свойство суммы углов треугольника, мы можем вычислить, что градусная мера угла ABD равна 180° - 70° - 80° = 30°.

Итак, градусная мера угла ABD равна 30°.