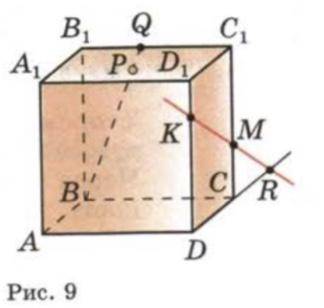
По рисунку 9 :б) плоскости в которых лежит прямая AA1; д) точки пересечения прямых MK и DC, B1C1 и BP, C1M и DC

Привет! Я рад, что ты обратился ко мне за помощью в решении этой задачи. Давай разберем ее по порядку.

Пункт а) не был озвучен, но я предполагаю, что нам нужно найти плоскости, в которых лежит прямая AA1. Чтобы найти такие плоскости, нам нужно знать, какая точка определяет прямую, а также направляющий вектор прямой.

Из рисунка мы видим, что прямая AA1 проходит через точку A и A1. Значит, эти точки определяют прямую. Но нам необходим направляющий вектор прямой, чтобы найти плоскости, в которых она лежит.

Чтобы найти направляющий вектор, возьмем две точки на прямой: A и A1. Затем вычтем их координаты, чтобы получить направляющий вектор. Пусть A = (x1, y1, z1) и A1 = (x2, y2, z2), тогда направляющий вектор можно найти как (x2 - x1, y2 - y1, z2 - z1).

Теперь у нас есть точка и направляющий вектор прямой AA1. Чтобы найти плоскости, в которых она лежит, нам нужно взять все возможные комбинации координатных плоскостей (xy, yz, xz) и подставить значения точки и направляющего вектора в общее уравнение плоскости.

Общее уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C и D - некоторые коэффициенты, а x, y и z - координаты точки. Если мы подставим значения точки и направляющего вектора в это уравнение, то получим уравнение плоскости.

Пункты б), д) требуют найти точки пересечения прямых. Чтобы найти точки пересечения, мы должны решить систему уравнений, задающую прямые.

Например, для пункта д) первая прямая задана двумя точками MK = (x1, y1, z1) и DC = (x2, y2, z2), а вторая прямая задана точкой B1C1 = (x3, y3, z3) и точкой BP = (x4, y4, z4).

Выражение для x-координаты точки пересечения M будет следующим:
(x - x1) / (x2 - x1) = (y - y1) / (y2 - y1) = (z - z1) / (z2 - z1).

Аналогично, можем составить выражения для y и z координат точки пересечения.

Делая аналогичные выкладки для других точек, мы можем получить координаты точек пересечения прямых.

Надеюсь, я смог объяснить задачу и процесс ее решения достаточно понятным образом. Если у тебя возникнут еще вопросы или что-то не будет ясно, не стесняйся обратиться ко мне снова. Я всегда готов помочь!