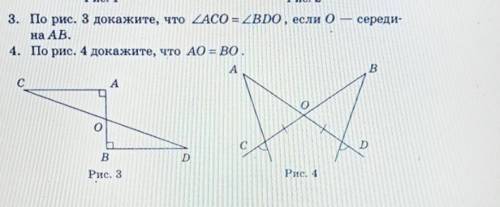
По рис. 3 докажите, что угол ACO = углу BDO, если 0 - середина AB.
По рис. 4 докажите, что АО = ВО.​

Дано:

СО=ОД

угол Д=углу С

1)угол С= углу Ф (обозначь его), т.к. эти углы вертикальные и они равны

угол Д=углу К (тоже обозначь), т.к. эти углы вертикальные и они равны

2) угол АОС=углу БОД, так как эти углы вертикальные

3) СО=ОД, отсюда следует, что треугольники АСО и ОБД равны по второму признаку равенства треугольников

4) соответственно АО=БО, т.к. треугольники равны, соответственно и элементы равны

Добрый день ученику! Благодарю за вопрос.

Для того чтобы доказать равенство углов ACO и BDO, мы можем использовать факт, что углы ACB и ADB равны между собой. Данный факт основан на том, что это вертикальные углы, образованные пересекающимися прямыми AB и CD.

Итак, начнем с рисунка 3. У нас есть угол ACO (указан в левом верхнем углу) и угол BDO (указан в правом верхнем углу).

Давайте рассмотрим треугольники ACO и BDO отдельно. Обратите внимание, что у нас есть два одинаковых угла: угол AOC и угол BOD. Это означает, что эти два треугольника являются подобными.

Поскольку треугольники ACO и BDO подобны, мы можем использовать свойство подобных треугольников: соответствующие стороны пропорциональны.

Мы знаем, что точка O является серединой отрезка AB (указано в условии), поэтому AO и BO равны между собой. Это означает, что стороны AO и BO одинаковы.

Теперь вернемся к углам ACO и BDO. Поскольку треугольники ACO и BDO оказались подобными, соответствующие углы этих треугольников также равны. Это означает, что угол ACO равен углу BDO.

Таким образом, угол ACO равен углу BDO.

Теперь перейдем к рисунку 4. Нам нужно доказать, что AO равно BO.

На этом рисунке у нас есть две вертикальные стороны AB и CD (указано в условии), а также две стороны AO и BO, которые являются радиусами.

Так как эти стороны являются радиусами окружности, то они равны между собой. Таким образом, AO равно BO.

Таким образом, мы доказали, что AO равно BO.

Я надеюсь, что мои объяснения были четкими и понятными. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!