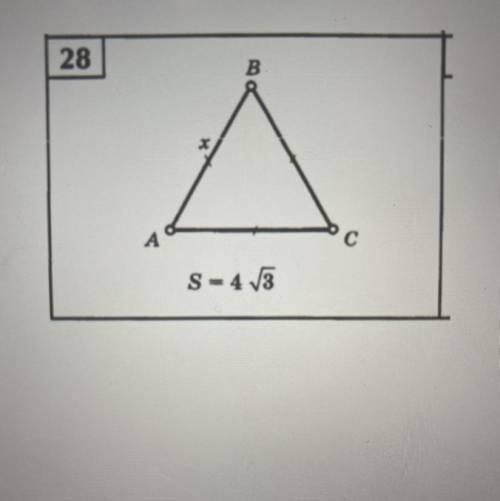
По данным рисунка найдите х

Чтобы найти значение х, необходимо использовать информацию, представленную на рисунке.

На данном рисунке представлена треугольная фигура, где одна из сторон является продолжением другой. Для нахождения значения х, нужно определить соотношение между данными углами.

Для начала обратим внимание на прямой угол, обозначенный как 90°. В таком угле сумма двух противолежащих углов равна 180°. Таким образом, угол ABF равен (180 - 90) = 90°.

Теперь обратим внимание на треугольник ABC. В сумме углы треугольника равны 180°. Отсюда можно найти угол ВАС, который равен (180 - 90) = 90°.

Зная, что угол ВАС равен 90°, и угол ABF также равен 90°, мы можем заключить, что треугольник ABF - прямоугольный треугольник. В прямоугольных треугольниках гипотенуза является наибольшей стороной и находится против угла 90°.

Исходя из этого, мы можем установить, что сторона фигуры, обозначенная как х, является гипотенузой треугольника ABF.

Теперь обратим внимание на другую информацию, представленную на рисунке. Сторона AB равна 6 и сторона AF равна 8.

Используя теорему Пифагора для прямоугольного треугольника ABF, мы можем получить следующее уравнение:
AB² + AF² = х²

Заменим известные величины в уравнение:
6² + 8² = х²
36 + 64 = х²
100 = х²

Чтобы найти значение х, необходимо найти квадратный корень из обеих частей уравнения:
√100 = √х²
10 = х

Таким образом, значение х равно 10.

Получившееся решение было получено путем использования геометрической информации, представленной на рисунке, а также применение теоремы Пифагора для прямоугольного треугольника. Результатное значение х равно 10 и подтверждается рассмотрением углов и сторон треугольника.