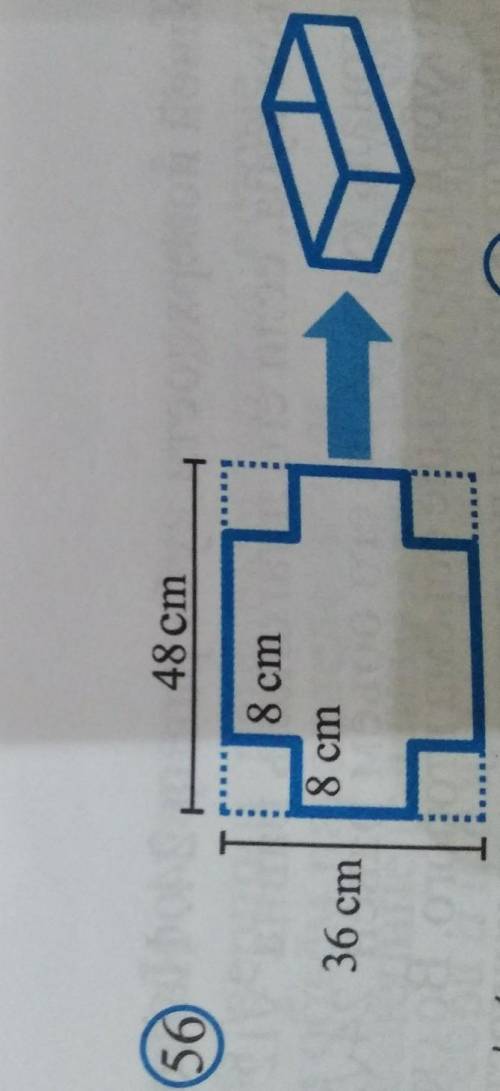
По данным развертки на рисунке 56 найдите объем получающегося из нее сосуда​

Для нахождения объема сосуда, получаемого из данной развертки, мы должны знать форму и размеры сосуда. Однако на данном рисунке мы видим только развертку, а не сам сосуд. Поэтому, чтобы решить эту задачу, мы должны разобрать развертку на составные части и вычислить объем каждой из них в отдельности.

Начнем с разбора развертки на составные части. По изображению видно, что развертку можно разделить на 3 прямоугольные части и один треугольный клин.

Для прямоугольных частей, мы можем найти объем прямоугольного параллелепипеда, используя формулу V = l × w × h, где l - длина, w - ширина и h - высота.

Рассмотрим первую (верхнюю) прямоугольную часть. На рисунке она обозначается цифрой 1. По измерениям на рисунке, длина l1 равна 20 см, ширина w1 равна 6 см, а высота h1 равна 2 см. Теперь мы можем подставить эти значения в формулу и вычислить объем:
V1 = l1 × w1 × h1 = 20 см × 6 см × 2 см = 240 см³

Аналогичным образом, найдем объем второй (средней) прямоугольной части. На рисунке она обозначается цифрой 2. Ее размеры: l2 = 10 см, w2 = 6 см, h2 = 4 см. Вычислим объем:
V2 = l2 × w2 × h2 = 10 см × 6 см × 4 см = 240 см³

Наконец, найдем объем третьей (нижней) прямоугольной части, обозначенной на рисунке цифрой 3. Размеры этой части: l3 = 20 см, w3 = 6 см, h3 = 2 см. Вычисляем объем:
V3 = l3 × w3 × h3 = 20 см × 6 см × 2 см = 240 см³

Теперь перейдем к треугольному клину, обозначенному цифрой 4 на развертке. Для вычисления его объема, нам понадобится знать формулу объема пирамиды: V = (1/3) × S × h, где S - площадь основания, а h - высота.

На рисунке видно, что треугольная основа клина имеет стороны, равные 20 см и 10 см, а высота h4 равна 4 см. Для вычисления площади основания, мы можем использовать формулу площади треугольника: S = (1/2) × a × b, где a и b - стороны треугольника.

Вычислим площадь основания клина:
S4 = (1/2) × 20 см × 10 см = 100 см²

Теперь можем подставить все значения в формулу объема пирамиды и вычислить объем клина:
V4 = (1/3) × S4 × h4 = (1/3) × 100 см² × 4 см = 133.33 см³

Чтобы найти общий объем получившегося сосуда, нужно просто сложить объемы всех составляющих его частей:
Общий объем = V1 + V2 + V3 + V4 = 240 см³ + 240 см³ + 240 см³ + 133.33 см³ ≈ 853.33 см³

Итак, мы получили, что объем получающегося из данной развертки сосуда составляет приблизительно 853.33 см³.