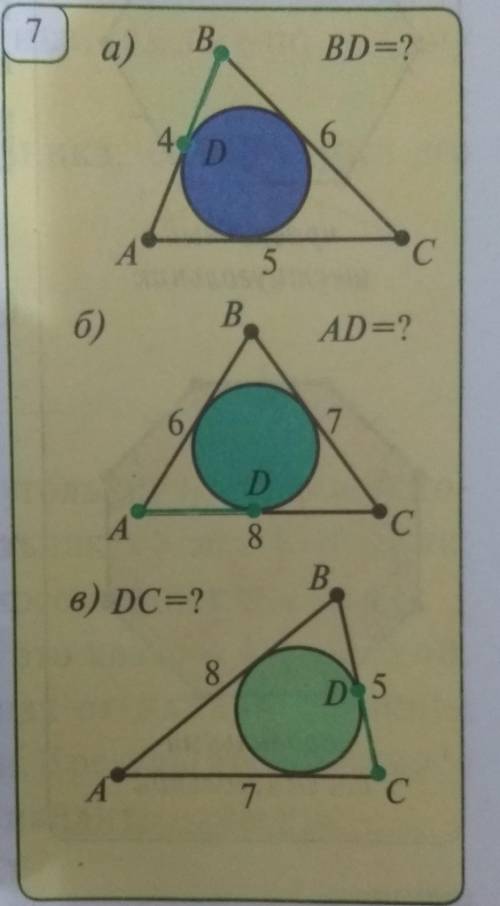
По данным на рисунке 7 найдите искомый отрезок​

а =2 б= 4 в=2.5

На рисунке 7 мы видим два отрезка - один прямой, обозначенный от точки А до точки В, и второй, косой отрезок, обозначенный от точки С до точки D. Чтобы найти искомый отрезок, нам необходимо использовать информацию, представленную на рисунке.

Давайте подробно разберемся, как найти искомый отрезок:
1. Обратимся к отрезку AB. Мы видим, что он имеет длину 4 единицы (обозначено правее от точки A). Поэтому длина отрезка AB равна 4.

2. Теперь обратимся к отрезку CD. Нам дан угол α, обозначенный справа от точки C. Угол α составляет 60 градусов. Это важно, чтобы мы могли найти искомый отрезок.

3. Давайте использовать тригонометрическую функцию синус. По определению, синус угла равен отношению противолежащей стороны к гипотенузе. В данном случае, отрезок CD является противолежащей стороной, а искомый отрезок является гипотенузой.

4. Найдем длину отрезка CD с помощью тригонометрии. Зная, что длина отрезка AB равна 4, мы можем использовать следующую формулу: CD = AB * sin(α), где sin(α) - синус угла α.

5. Подставляя значения, получаем: CD = 4 * sin(60°).

6. Теперь, чтобы получить точное значение искомого отрезка, мы должны найти значение sin(60°). Справедливо, что sin(60°) = √3/2. Значит, мы можем заменить sin(60°) на √3/2 и продолжить вычисления.

7. Раскрываем выражение: CD = 4 * √3/2.

8. Сокращаем числитель и знаменатель: CD = 2√3.

Таким образом, искомый отрезок CD равен 2√3 единицам.