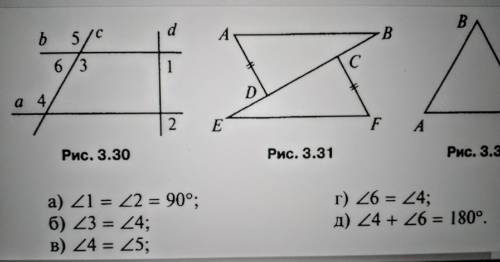
По чертежу 3.30. ответить на вопрос: "Параллельны ли прямые "a" и "b"?

ответы обосновать.

Пункты:

а,б,в,г,д

Для того чтобы определить, являются ли прямые "a" и "b" параллельными, нужно применить знания о свойствах параллельных прямых. В данном случае нам дано изображение чертежа, на котором находятся эти две прямые.

Первым шагом для решения этой задачи мы должны определить, какие свойства параллельных прямых мы можем использовать для доказательства. Одно из таких свойств гласит, что если две прямые пересекаются третьей прямой, и углы, образованные этой третьей прямой со сторонами пересекающихся прямых, равны между собой, то пересекаемые прямые параллельны.

Посмотрим на чертеж 3.30. Обратим внимание, что прямые "a" и "b" пересекаются третьей прямой, обозначенной как "m". Теперь мы можем посмотреть на углы, образованные третьей прямой "m" со сторонами пересекающихся прямых "a" и "b".

На чертеже в пунктах "а", "б", "в", "г" и "д" указаны различные углы, образованные третьей прямой "m" со сторонами "a" и "b". Нам нужно посмотреть, являются ли эти углы одинаковыми между собой. По изображению можно заметить, что все углы, обозначенные в пунктах "а", "б", "в", "г" и "д", равны между собой.

Таким образом, по свойству параллельных прямых мы можем сделать вывод, что прямые "a" и "b" параллельны друг другу. Основанием для этого объяснения служит равенство углов, образованных третьей прямой "m" со сторонами "a" и "b" в данном чертеже.

Ответ: Прямые "a" и "b" являются параллельными. Это можно сделать вывод на основании равенства углов, образованных третьей прямой "m" со сторонами "a" и "b". Поэтому ответом будет пункт "г".